ML Interview Essentials: Building Multi-Head Self-Attention

#5: Multi-head Self-Attention

We built Self-attention from scratch in a previous lesson in this series on ML interview essentials.

ML Interview Essentials: Building Self-Attention From Scratch

Here’s the next step we take from there and build the Multi-Head Self-Attention (MHA).

Let’s begin!

---

Before we start, I want to introduce you to the Visual Tech Bundle.

It is a collection of visual guides that explain core AI, LLM, Systems design, and Computer science concepts via image-first lessons.

Others are already loving these books. Why not give them a try?

---

Revisiting Self-Attention

Before we move forward, let’s quickly recap what we built in the previous lesson.

Following is the SelfAttention class that represents the Scaled Dot-product Self-attention, and does the following operations:

• Accepts input embeddings (x) as input

• Projects them into Queries (Q), Keys (K), and Values (V) using learnable projection matrices specific to each one of them

• Computes attention scores (Q * K^T)

• Scales and applies softmax to the attention scores to get attention weights

• Multiplies the attention weights by Values (V) and returns the output

import torch
import torch.nn as nn

class SelfAttention(nn.Module):
    def __init__(self, embedding_dim):
        super().__init__()
        self.embedding_dim = embedding_dim
        
        # Learnable projection matrices for Q, K, V
        self.W_q = nn.Linear(embedding_dim, embedding_dim, bias=False)
        self.W_k = nn.Linear(embedding_dim, embedding_dim, bias=False)
        self.W_v = nn.Linear(embedding_dim, embedding_dim, bias=False)
    
    def forward(self, x):
        # Project input to Q, K, V
        Q = self.W_q(x)  
        K = self.W_k(x)  
        V = self.W_v(x) 
        
        # Calculate Attention scores
        attn_scores = Q @ K.transpose(-2, -1) 
        
        # Scale and apply softmax to get Attention weights
        attn_weights = torch.softmax(attn_scores / self.embedding_dim**0.5, dim=-1)
        
        # Multiply Attention weights by values (V)
        output = attn_weights @ V  
        
        return output

---

Extending To Multi-head Attention

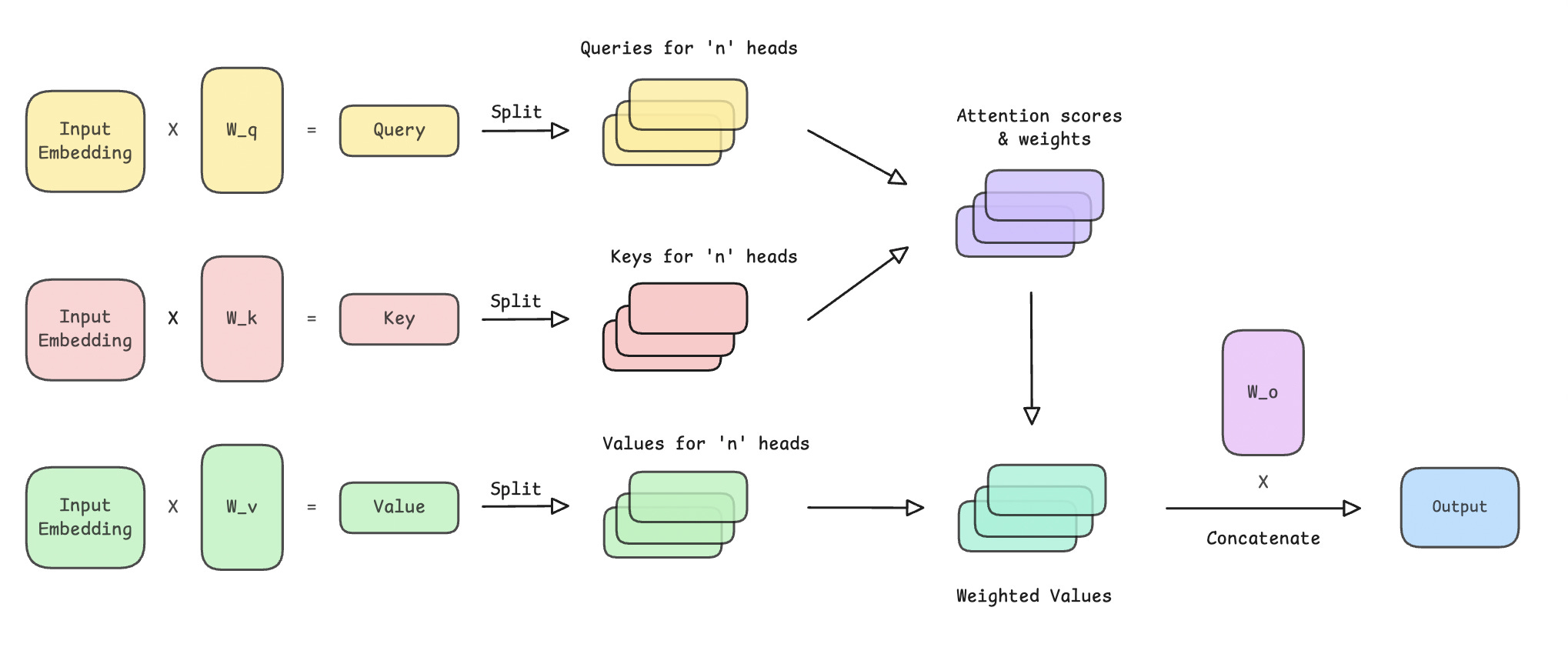
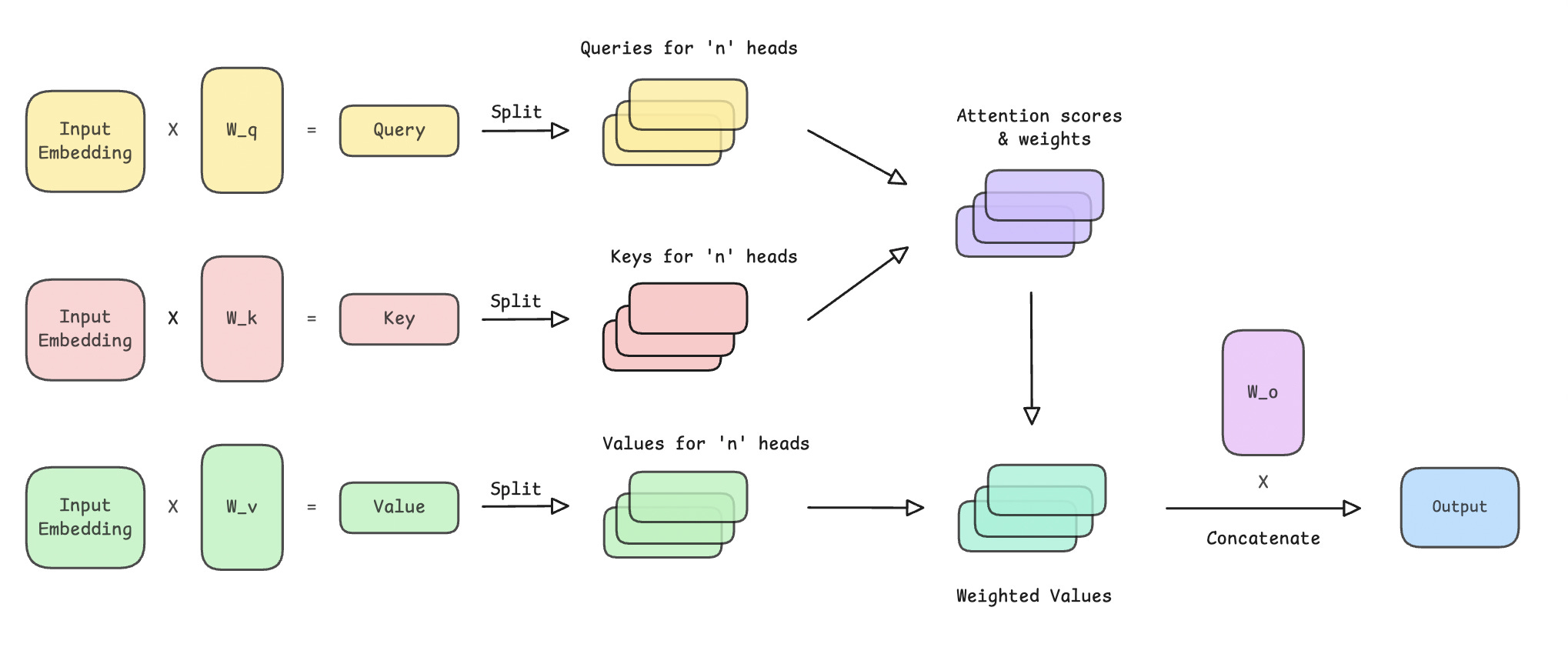
Multi-head attention (MHA) extends self-attention by using multiple parallel self-attention blocks, or heads, rather than just one.

Each head starts with different learned projections for Queries (Q), Keys (K), and Values (V) and are used to better learn different types of semantic relationships within the input embeddings.

The outputs of these heads are finally concatenated and linearly transformed using another projection matrix to obtain the final output.

The steps will become much clearer when we write the forward pass of MHA.

Let’s first create input embeddings that MHA will process.

import torch 

batch_size = 10
sequence_length = 6
embedding_dim = 12

# Create embeddings for a batch
input_embeddings = torch.rand(batch_size, sequence_length, embedding_dim)

Next, we implement MHA as the MultiHeadSelfAttention class as follows.

import torch.nn as nn 
import math 

class MultiHeadSelfAttention(nn.Module):
  def __init__(self, embedding_dim, num_heads):
    super().__init__()
    
    # Check if embedding_dim is divisible by num_heads
    assert embedding_dim % num_heads == 0, “embedding_dim must be divisible by num_heads”

    # Embedding dimension
    self.embedding_dim = embedding_dim 

    # Number of total heads
    self.num_heads = num_heads
    
    # Dimension of each head
    self.head_dim = embedding_dim // num_heads 

    # Linear projections for Q, K, V (to be split later for each head)
    self.W_q = nn.Linear(embedding_dim, embedding_dim, bias = False)
    self.W_k = nn.Linear(embedding_dim, embedding_dim, bias = False)
    self.W_v = nn.Linear(embedding_dim, embedding_dim, bias = False)

    # Linear projection to produce final output
    self.W_o = nn.Linear(embedding_dim, embedding_dim, bias = False)

  def _split_heads(self, x):
    “”“
    Transforms input embeddings from 
    [batch_size, sequence_length, embedding_dim]
    to  
    [batch_size, num_heads, sequence_length, head_dim]
    “”“
    batch_size, sequence_length, embedding_dim = x.shape
    
     # Split embedding_dim into (num_heads, head_dim)
    x = x.reshape(batch_size, sequence_length, self.num_heads, self.head_dim)
    
    # Reorder and return the intended shape
    return x.transpose(1,2) 

  def _merge_heads(self, x):
    “”“
    Transforms inputs from 
    [batch_size, num_heads, sequence_length, head_dim]
    to 
    [batch_size, sequence_length, embedding_dim]
    “”“
    batch_size, num_heads, sequence_length, head_dim = x.shape
    
    # Move sequence_length back before num_heads in the shape
    x = x.transpose(1,2) 
    
    # Merge (num_heads, head_dim) back into embedding_dim
    embedding_dim = num_heads * head_dim
    x = x.reshape(batch_size, sequence_length, embedding_dim)

    return x

  def forward(self, x):
    batch_size, sequence_length, embedding_dim = x.shape

    # Compute Q, K, V
    Q = self.W_q(x)  
    K = self.W_k(x)  
    V = self.W_v(x)
    
    # Split them into multiple heads 
    Q = self._split_heads(Q)
    K = self._split_heads(K)
    V = self._split_heads(V)

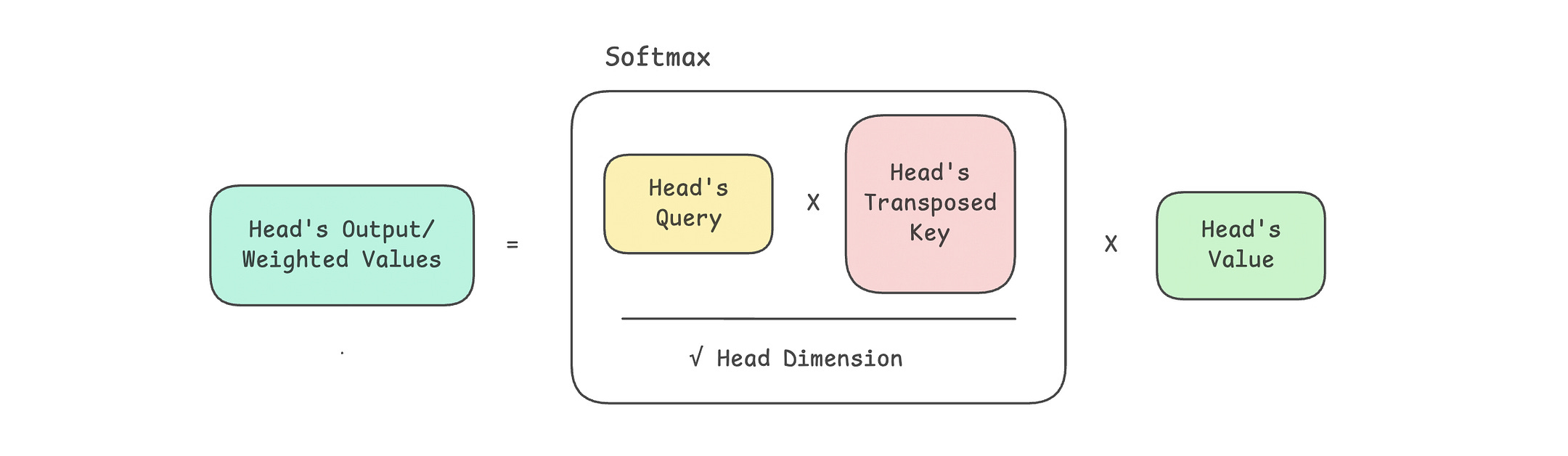
    # Calculate scaled dot-product attention
    attn_scores = Q @ K.transpose(-2, -1)
    
    # Scale and apply softmax to get attention weights
    attn_scores = attn_scores / math.sqrt(self.head_dim)
    attn_weights = torch.softmax(attn_scores, dim = -1)
    
    # Multiply attention weights by values (V)
    weighted_values = attn_weights @ V 

    # Merge heads 
    merged_heads_output = self._merge_heads(weighted_values) 

    # Final output
    output = self.W_o(merged_heads_output)

    return output

---

Let’s use it to process the input embeddings that we created previously.

# Set number of heads 
NUM_HEADS = 3

# Initialize MHA 
mha = MultiHeadSelfAttention(embedding_dim, num_heads = NUM_HEADS)

# Forward pass 
output = mha(input_embeddings)

Note that MHA preserves the shape of the input ([batch_size, sequence_length, embedding_dim]). This lets us stack multiple MHA layers together in a Transformer block.

print(”Input shape:”, input_embeddings.shape)
print(”Output shape:”, output.shape)

“”“
Input shape: torch.Size([10, 6, 12])
Output shape: torch.Size([10, 6, 12])
“”“

---

This is how the operations in MHA look.

The detailed calculations of attention scores and weights, along with the resulting weighted values, are shown in the following image.

---

That’s everything for this article.

It is entirely free to read. If you loved reading it, restack and share it with others.

---

You can read the other articles in this series using the links below.

• Building Self-Attention From Scratch: https://intoai.pub/self-attention

• What Is Normalization?: https://intoai.pub/normalization

• What is Gradient Descent?: https://intoai.pub/p/gradient-descent

• K-Nearest Neighbours (KNN): https://intoai.pub/p/knn

---

If you want to get even more value from this publication, consider becoming a paid subscriber.

You can also check out my books on Gumroad and connect with me on LinkedIn to stay in touch.