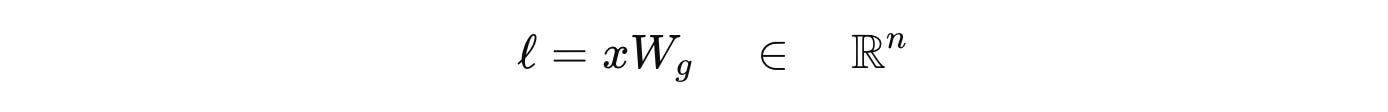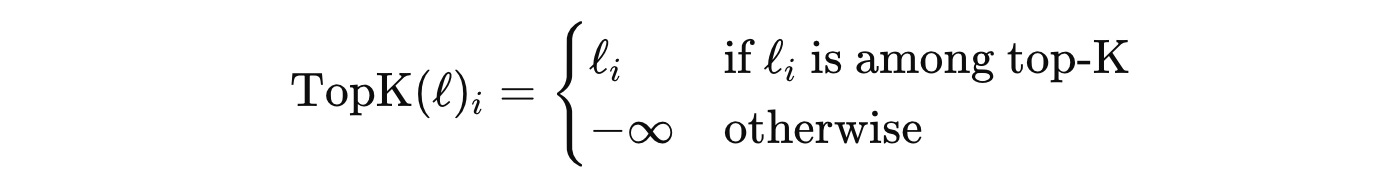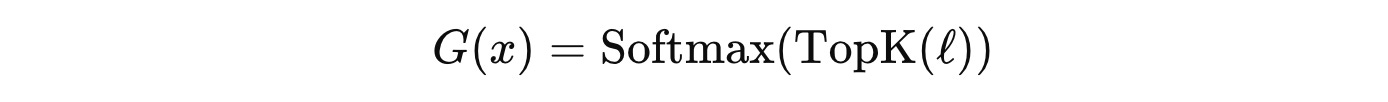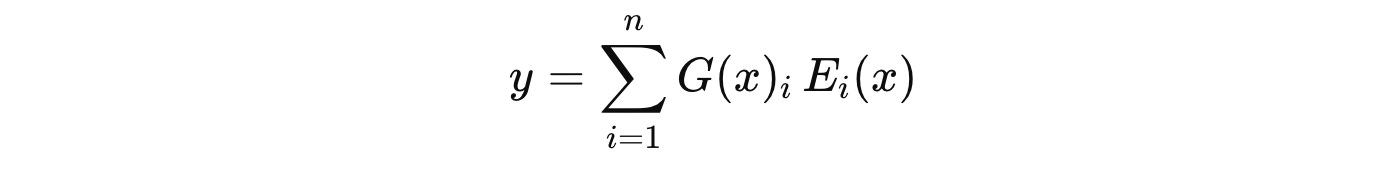Build a Mixture-of-Experts (MoE) LLM from Scratch (Part-1)
Learn to build the Mixture-of-Experts (MoE) layer that powers LLMs like gpt-oss, Grok, and Mixtral from scratch in PyTorch.
🎁 Become a paid subscriber to ‘Into AI’ today at a special 25% discount on the annual subscription.
In the previous lesson on ‘Into AI’, we learned how to build the Decoder-only Transformer from scratch and trained an LLM that used it on a dataset of Wikipedia articles.
Modern-day LLMs like Grok-1, DeepSeekMoE, gpt-oss, and Mixtral (and many other proprietary LLMs whose architectural details aren’t publicly available) use the Mixture of Experts (MoE) architecture.
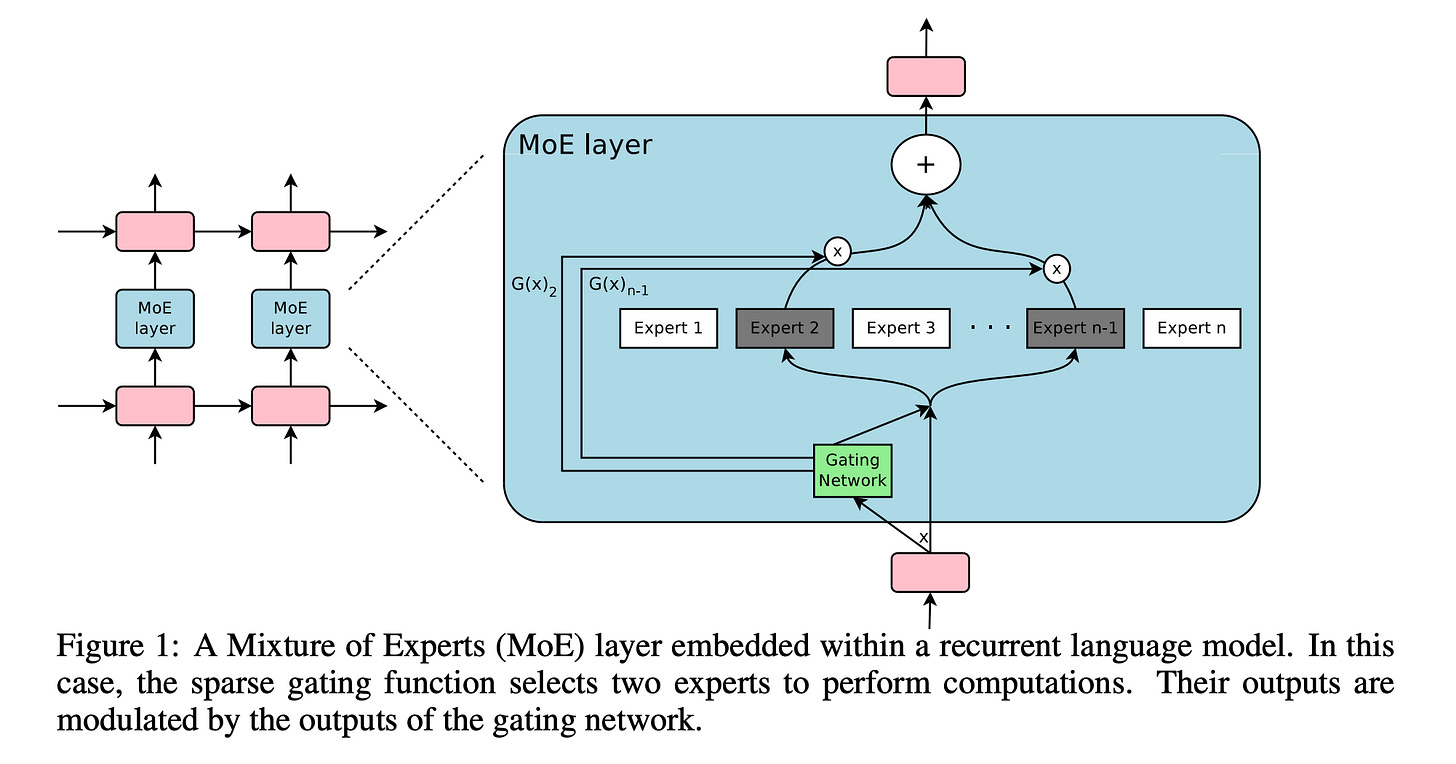
This architecture was popularly introduced in the research paper titled “Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer” by Shazeer et al.

The authors of this paper applied the MoE architecture to RNNs with LSTM layers, rather than LLMs of today.
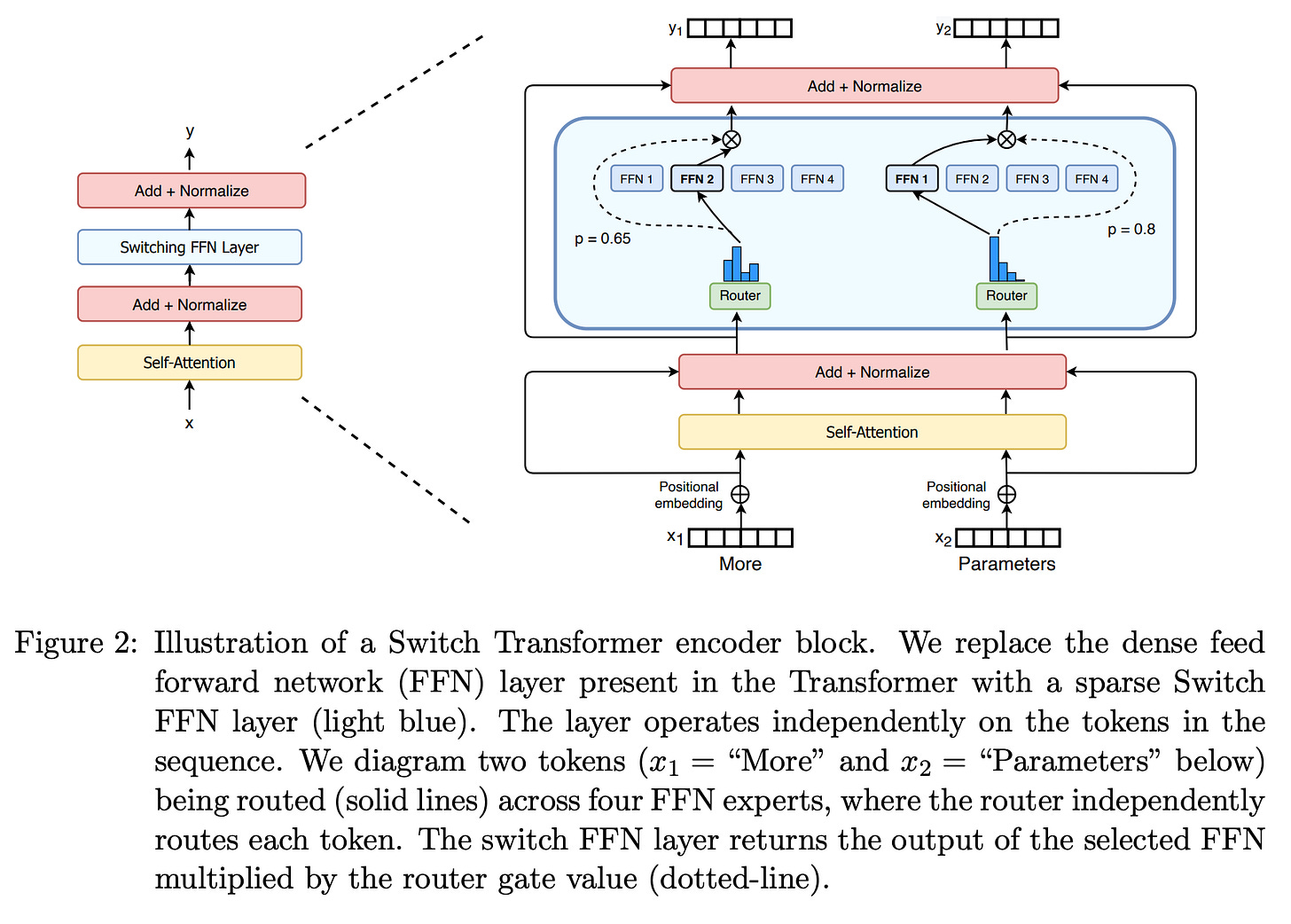
It was later in 2021 that the Switch Transformer paper by Fedus et al. applied the MoE architecture to the Transformer.
In this article, we will learn about:
What the Mixture of Experts (MoE) architecture is
What are its benefits, and why is it so popularly used in modern LLMs
Build our own MoE layer from scratch in PyTorch
Let’s begin!
Before we move forward, I want to introduce you to the Visual Tech Bundle.
It is a collection of visual guides that explain core AI, LLM, Systems design, and Computer science concepts via image-first lessons.
Others are already loving these books.
This includes Dharmesh Shah, the co-founder and CEO of HubSpot.
Why not give them a try?
Now back to our lesson!
What is the Mixture of Experts (MoE) architecture?
In previous lessons, we learned how the Decoder-only transformer makes text generation possible.
Its components are as follows:
Causal (or Masked) Multi-Head Self-Attention
Feed-Forward Network (FFN)
Layer Normalization
Residual or Skip connections
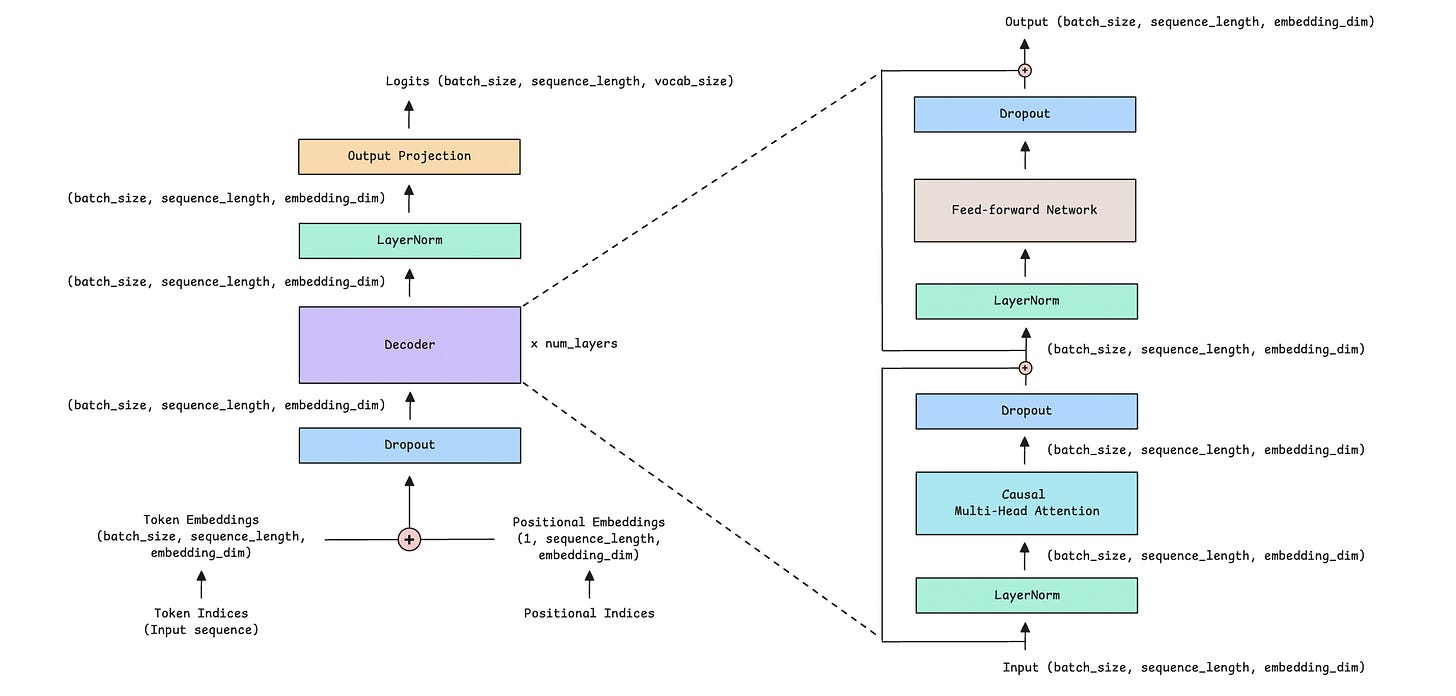
Note the large feed-forward network in this architecture (shown as a gray block), which processes each token in the input sequence. This is a computationally intensive part of the original Transformer architecture.
The MoE architecture addresses this by replacing the large feed-forward network with multiple small feed-forward networks, each with its own independent weights. Each of these small networks is called an Expert.
Each of these Experts specializes in a particular skill, which may involve processing different token types (numerical/code/language-related tokens), reasoning patterns, context patterns, and so on.
Such specialization isn’t hard-coded into the architecture. Instead, it develops as an MoE LLM trains.
A Routing network/Gating network/Router is another small feed-forward neural network in the architecture that decides which expert should process which token in the input sequence.
Given a token’s embedding in the input sequence, the router:
Outputs a score for each expert (which becomes a weight after softmax)
Selects the top-k experts (‘k’ is the number of experts activated per token)
Routes the token only to those experts
This means that not every token passes through a large feed-forward neural network, as in the conventional Decoder-only Transformer, but instead through smaller networks determined by the router.
This enables sparse computation of tokens and significantly reduces computational requirements.
Once processed by the experts, their outputs are weighted by the router’s softmax scores/weights, summed to form a single combined representation, and forwarded to the next layer of the Transformer.
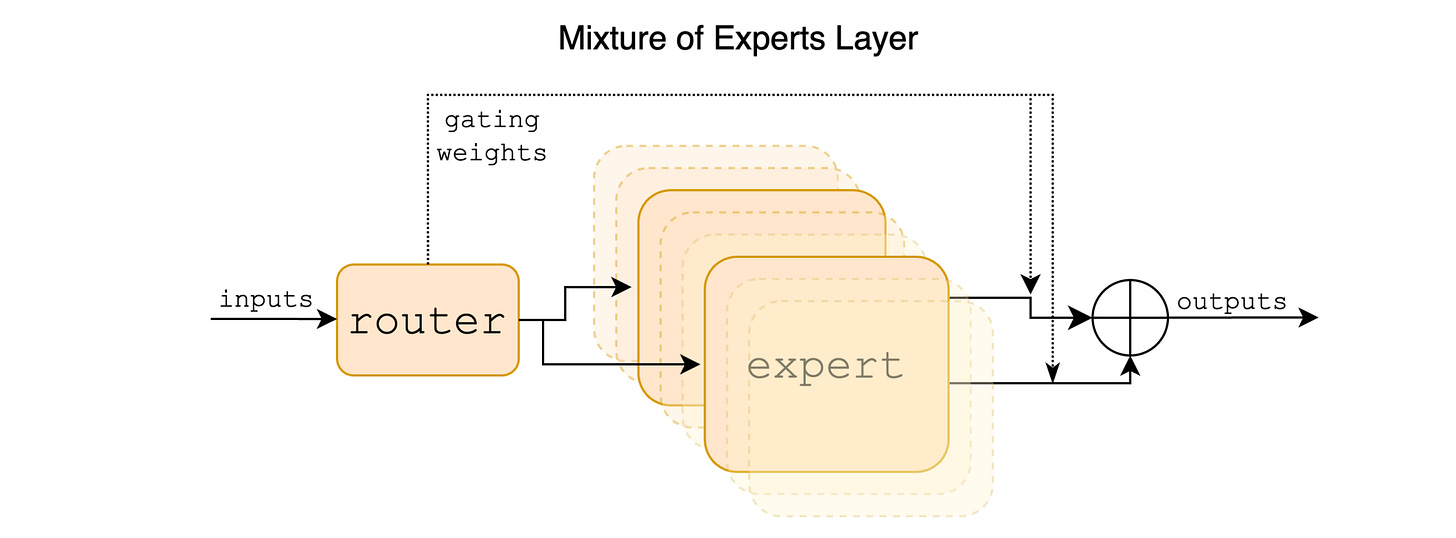
Both the experts and the router form the Mixture of Experts (MoE) layer, which acts as a drop-in replacement of the large Feed-forward network in the conventional Decoder-only Transformer.
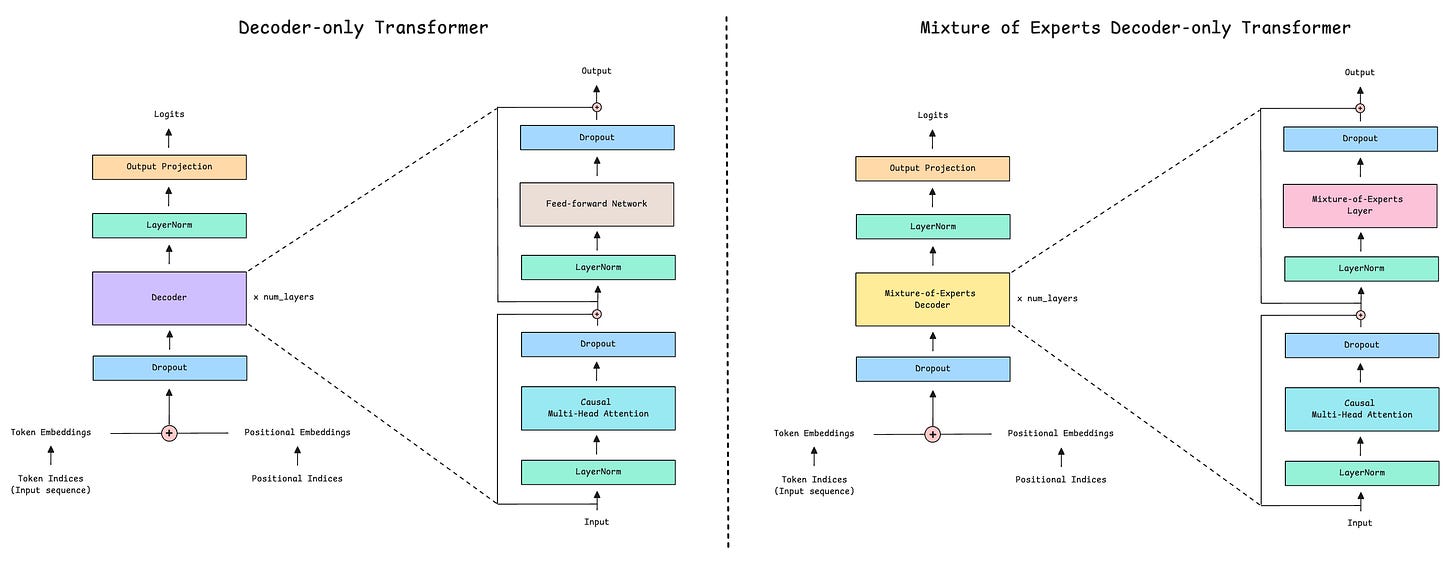
Let’s go a bit deeper and examine the mathematical details of the MoE layer to understand it better.
The Mathematics Behind the Mixture of Experts (MoE) Layer
Let’s understand what happens inside a MoE layer step by step.
Step 1: Compute Router logits
Given the token embeddings input to the MoE layer represented by ‘x’ and ‘n’ as the total number of Experts, the router computes a score/ logit for each expert using a linear projection W(g) as follows:
where l(i) is the logit for expert i.
Step 2: Select logits for top-k experts and mask out the rest
Based on ‘k’, a hyperparameter that represents the number of experts activated per token, the logits for only the top-k experts are kept, and the rest are masked out using -∞.
(Remember, we did the same when building Causal Multi-head Self-attention?)
Step 3: Apply Softmax
After top-k masking, applying softmax assigns zero probability to non-selected experts (whose logits are set to −∞ in the previous step) and normalizes the selected experts’ weights so that they sum to 1.
Step 4: Compute using experts and aggregate their outputs
Each selected expert processes the token independently, and the final output ‘y’ is computed as a weighted sum of the experts’ outputs, where each expert is denoted by E(i).
These equations will become much clearer once we implement the MoE layer in the next section.
Building the MoE Layer in PyTorch
Let’s code up the MoE layer in PyTorch to better understand how it works.
To keep this tutorial easy to understand, we will build our MoE layer in a manner similar to the simpler Mixtral 8x7B architecture.
Our MoE layer consists of:
Multiple Experts
A Router
Note that many newer LLMs, like DeepSeekMoE, use a hybrid approach with experts that can have two types:
Shared experts: These are always activated for every token
Routed experts: Conditionally activated via top-k routing as discussed above
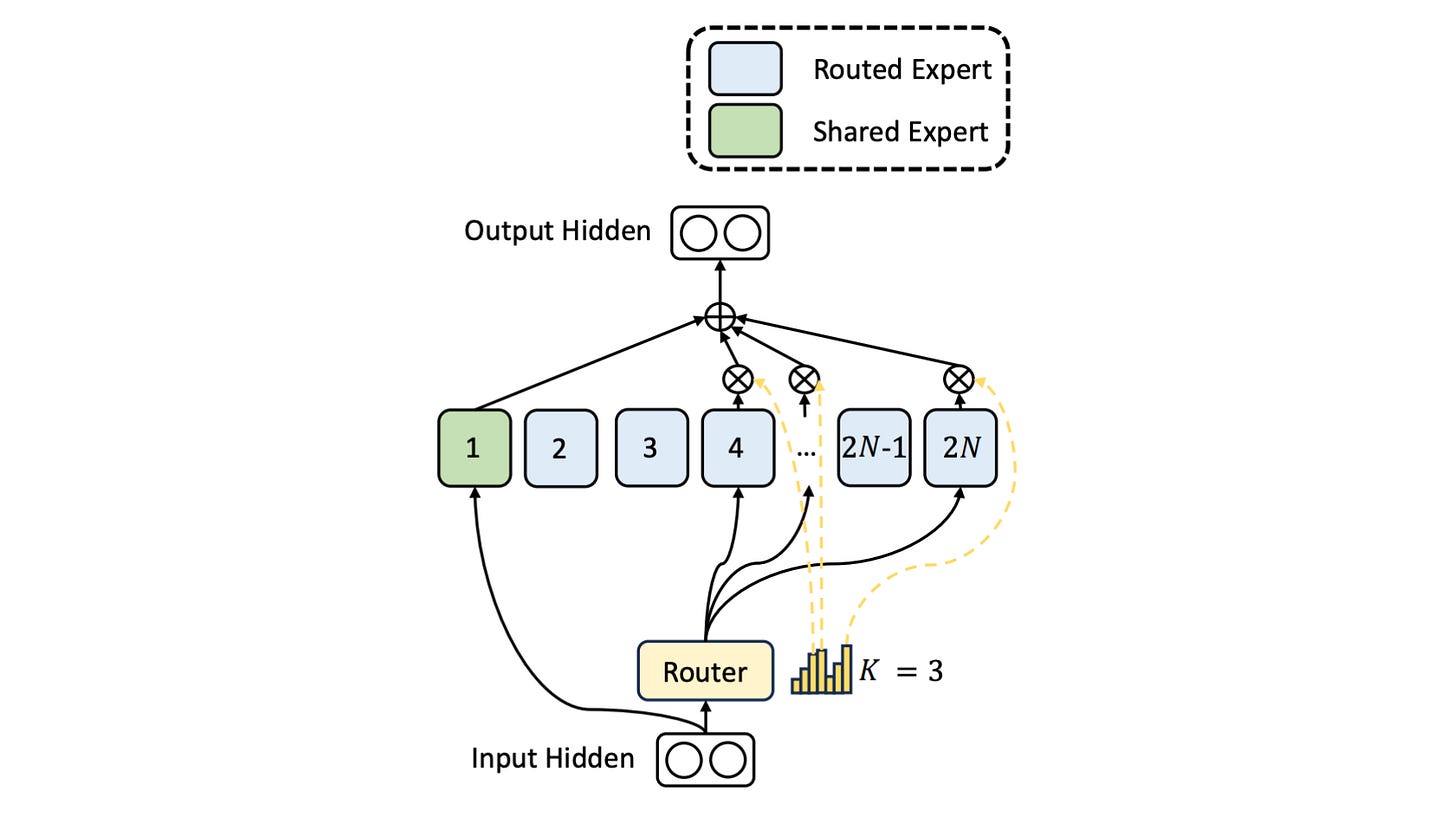
We aren’t building such an architecture in this tutorial, and sticking to a simpler one with no shared experts.
Building the Experts