Build Multi-Query Attention (MQA) From Scratch

AI Engineering Essentials: Learn to implement Multi-Query Attention (MQA) used in LLMs like PaLM and Falcon from scratch

In the previous lessons on 'Into AI’, we learned to implement Self-attention and progressively updated it to reach Causal Multi-head Self-attention (MHA), which is used in LLMs like GPT-2.

Here are the lessons if you missed them:

Build Self-Attention From Scratch

Build Multi-Head Self-Attention From Scratch

Build Causal Multi-Head Self-Attention From Scratch

---

MHA is a powerful architectural component that enables LLMs to process tokens in parallel and makes fast autoregressive text generation possible.

But it comes with high memory costs and latency.

It was therefore made more efficient by Noam Shazeer in his research paper titled ‘Fast Transformer Decoding: One Write-Head is All You Need’.

This is where he introduces Multi-Query Attention (MQA), an efficient variant of MHA that significantly reduces memory usage and speeds up inference.

Source

---

What is Multi-Query Attention (MQA)?

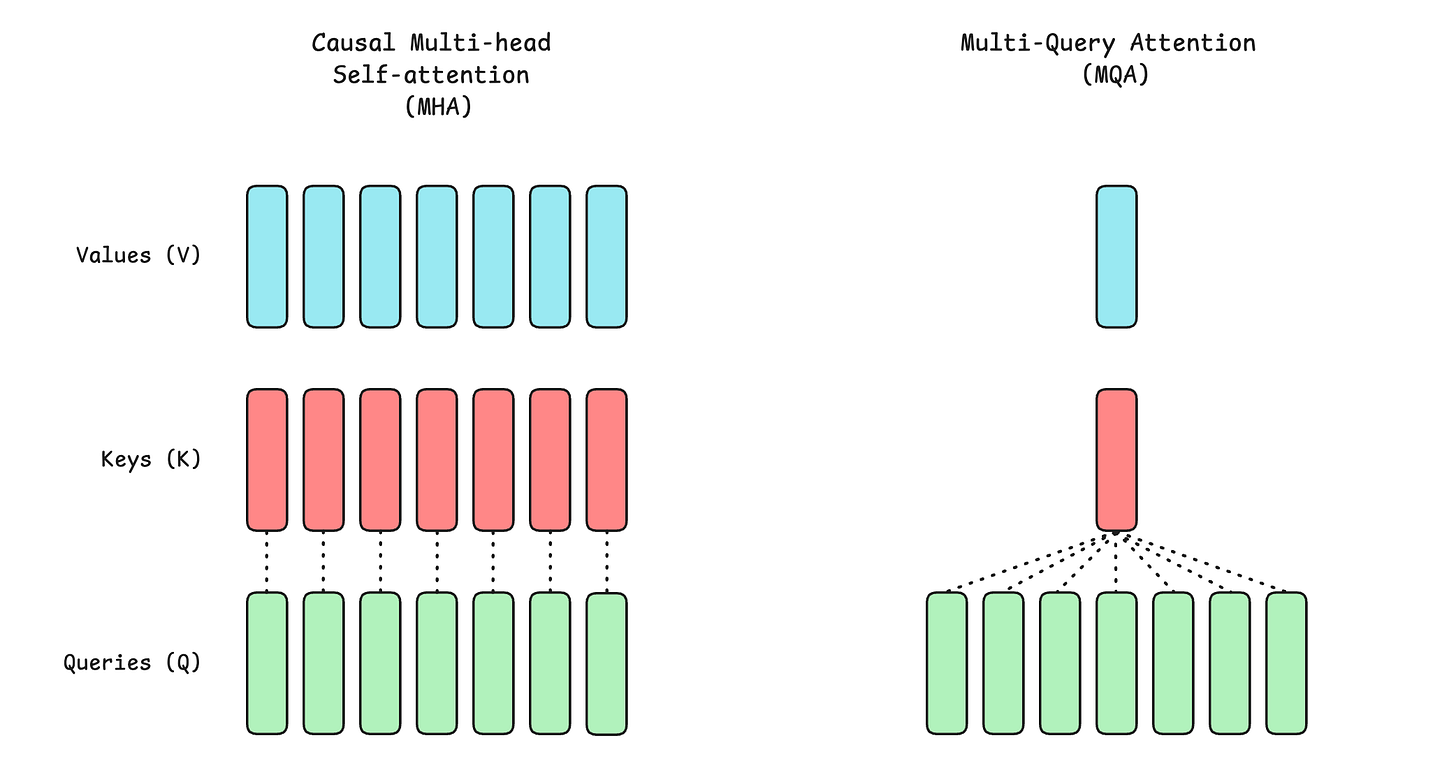
In the conventional attention or Causal Multi-Head Attention (MHA), each head has its own Q, K, and V vectors.

Operations in MHA

This means that the memory requirements grow with the number of heads.

In MQA, all attention heads share the same key (K) and value (V) vectors, while each head still has its own query (Q) vector.

This reduces the parameter count for K and V projection matrices and requires less activation memory during model training.

Although the training benefits aren’t particularly significant, the real benefits become clear during inference, as the KV cache size and required memory decrease significantly. This leads to much faster inference, especially for long sequences and large batch sizes, with little degradation in response quality.

Multi-Query Attention visualised (Image from author’s book titled ‘LLMs In 100 Images’)

LLMs like PaLM and Falcon use MQA instead of MHA.

Use of MQA in Google PaLM (Source)

---

Revisiting MHA

Multi-head Attention (MHA) is implemented with causal masking in LLMs, and this architecture is called Causal Multi-head Self-attention. This prevents an LLM from peeking at future tokens while generating a token.

(Note that Causal Multi-Head Self-Attention is usually just called MHA in the popular literature.)

We previously learned how to build Causal Multi-Head Self-Attention from scratch. Here’s a quick recap of how it works.

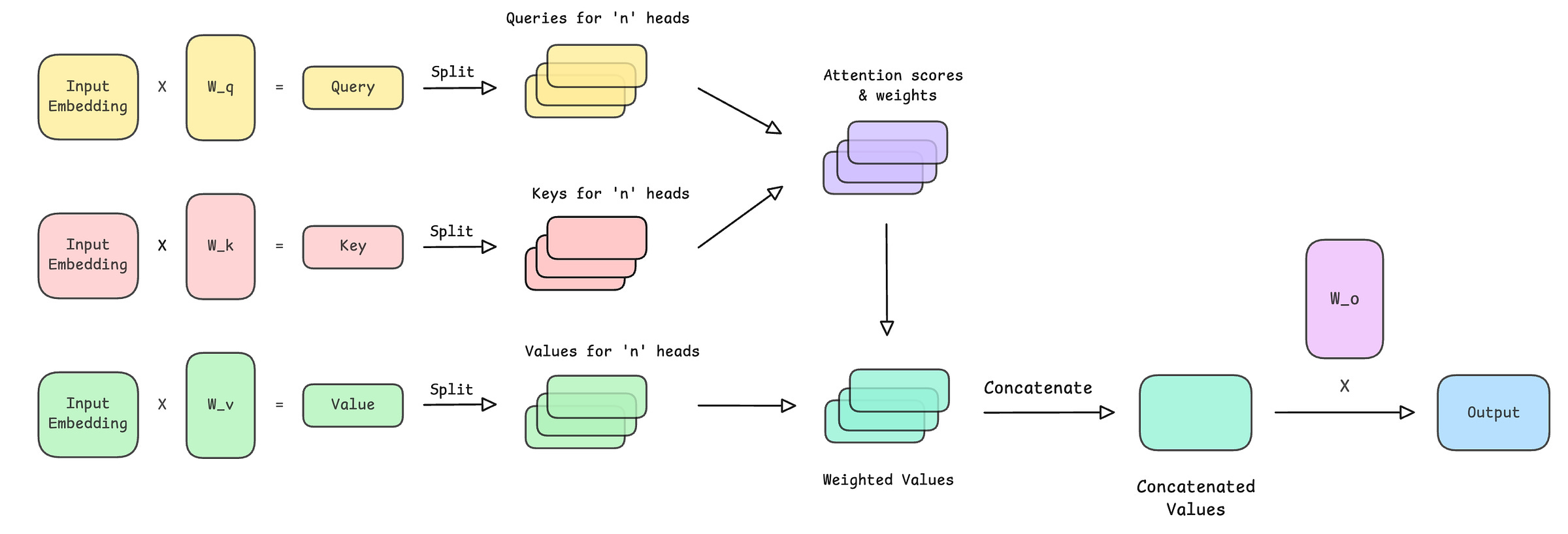
The following steps are performed in this class representing MHA:

• Input embeddings are projected into query (Q), key (K), and value (V) vectors

• Q, K, and V are split across multiple attention heads

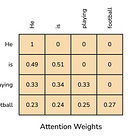
• Scaled dot-product attention is computed, and a causal mask is applied

• Softmax is applied to obtain attention weights

• Attention weights are used to compute a weighted sum of values (V) for each head

• The head outputs are merged and passed through a final output projection matrix

import torch
import torch.nn as nn
import math

class CausalMultiHeadSelfAttention(nn.Module):
  def __init__(self, embedding_dim, num_heads):
    super().__init__()

    # Check if embedding_dim is divisible by num_heads
    assert embedding_dim % num_heads == 0, “embedding_dim must be divisible by num_heads”

    # Embedding dimension
    self.embedding_dim = embedding_dim

    # Number of total heads
    self.num_heads = num_heads

    # Dimension of each head
    self.head_dim = embedding_dim // num_heads

    # Linear projection matrices for Q, K, V (to be split later for each head)
    self.W_q = nn.Linear(embedding_dim, embedding_dim, bias = False)
    self.W_k = nn.Linear(embedding_dim, embedding_dim, bias = False)
    self.W_v = nn.Linear(embedding_dim, embedding_dim, bias = False)

    # Linear projection matrix to produce final output
    self.W_o = nn.Linear(embedding_dim, embedding_dim, bias = False)

  def _split_heads(self, x):
    """
    Transforms input embeddings from
    [batch_size, sequence_length, embedding_dim]
    to
    [batch_size, num_heads, sequence_length, head_dim]
    """
    batch_size, sequence_length, embedding_dim = x.shape

    # Split embedding_dim into (num_heads, head_dim)
    x = x.reshape(batch_size, sequence_length, self.num_heads, self.head_dim)

    # Reorder and return the intended shape
    return x.transpose(1,2)

  def _merge_heads(self, x):
    """
    Transforms inputs from
    [batch_size, num_heads, sequence_length, head_dim]
    to
    [batch_size, sequence_length, embedding_dim]
    """
    batch_size, num_heads, sequence_length, head_dim = x.shape

    # Move sequence_length back before num_heads in the shape
    x = x.transpose(1,2)

    # Merge (num_heads, head_dim) back into embedding_dim
    embedding_dim = num_heads * head_dim
    x = x.reshape(batch_size, sequence_length, embedding_dim)

    return x

  def forward(self, x):
    batch_size, sequence_length, embedding_dim = x.shape

    # Compute Q, K, V
    Q = self.W_q(x)
    K = self.W_k(x)
    V = self.W_v(x)

    # Split them into multiple heads
    Q = self._split_heads(Q)
    K = self._split_heads(K)
    V = self._split_heads(V)

    # Calculate scaled dot-product attention
    attn_scores = Q @ K.transpose(-2, -1)

    # Scale
    attn_scores = attn_scores / math.sqrt(self.head_dim)

    # Apply causal mask (prevent attending to future positions)
    causal_mask = torch.tril(torch.ones(sequence_length, sequence_length, device=x.device)) # Create lower triangular matrix

    causal_mask = causal_mask.view(1, 1, sequence_length, sequence_length)  # Add batch and head dimensions
     
    attn_scores = attn_scores.masked_fill(causal_mask == 0, float(’-inf’)) # Mask out future positions by setting their scores to -inf

    # Apply softmax to get attention weights
    attn_weights = torch.softmax(attn_scores, dim = -1)

    # Multiply attention weights by values (V)
    weighted_values = attn_weights @ V

    # Merge head outputs
    merged_heads_output = self._merge_heads(weighted_values)

    # Final output
    output = self.W_o(merged_heads_output)

    return output 

---

Moving Towards MQA

As we discussed previously:

In Multi-Query Attention (MQA), all attention heads share the same key (K) and value (V) vectors, while each head still has its own query (Q) vector.

Again, we will implement the causal version of MQA, though in practice it is simply referred to as MQA in most of the popular literature.

Let’s implement it in the MultiQueryAttention class.

• We begin by setting the dimensions and creating projection matrices.

import torch
import torch.nn as nn
import math

class MultiQueryAttention(nn.Module):
  def __init__(self, embedding_dim, num_heads):
    super().__init__()

    # Check if embedding_dim is divisible by num_heads
    assert embedding_dim % num_heads == 0, "embedding_dim must be divisible by num_heads"

    # Embedding dimension
    self.embedding_dim = embedding_dim

    # Number of total heads
    self.num_heads = num_heads

    # Dimension of each head
    self.head_dim = embedding_dim // num_heads

    # Linear projection matrix for Query 
    self.W_q = nn.Linear(embedding_dim, embedding_dim, bias = False)

    # Linear projection matrices for Key and Value
    self.W_k = nn.Linear(embedding_dim, self.head_dim, bias = False)
    self.W_v = nn.Linear(embedding_dim, self.head_dim, bias = False)

    # Linear projection matrix to produce final output
    self.W_o = nn.Linear(embedding_dim, embedding_dim, bias = False)

Note how the output size is for the key and value projections is head_dim and not embedding_dim as in the case of the query projection.

This means that we create only one set of K and V vectors per token and then broadcast them across all heads later.

• Next, we define a function that splits the query into multiple heads

  # Splits Query into multiple heads
  def _split_heads(self, x):
    """
    Transforms input embeddings from
    [batch_size, sequence_length, embedding_dim]
    to
    [batch_size, num_heads, sequence_length, head_dim]
    """
    batch_size, sequence_length, embedding_dim = x.shape

    # Split embedding_dim into (num_heads, head_dim)
    x = x.reshape(batch_size, sequence_length, self.num_heads, self.head_dim)

    # Reorder and return the intended shape
    return x.transpose(1,2)

• We then define a function that merges the head outputs back

  # Merge heads back together
  def _merge_heads(self, x):
    """
    Transforms inputs from
    [batch_size, num_heads, sequence_length, head_dim]
    to
    [batch_size, sequence_length, embedding_dim]
    """
    batch_size, num_heads, sequence_length, head_dim = x.shape

    # Move sequence_length back before num_heads in the shape
    x = x.transpose(1,2)

    # Merge (num_heads, head_dim) back into embedding_dim
    embedding_dim = num_heads * head_dim
    x = x.reshape(batch_size, sequence_length, embedding_dim)

    return x

• Finally, the forward pass is defined as follows.

  # Forward pass
  def forward(self, x):
    batch_size, sequence_length, embedding_dim = x.shape

    # Compute Q, K, V
    Q = self.W_q(x) # [batch_size, sequence_length, embedding_dim]
    K = self.W_k(x) # [batch_size, sequence_length, head_dim]
    V = self.W_v(x) # [batch_size, sequence_length, head_dim]

    # Split Q into multiple heads
    Q = self._split_heads(Q) # [batch_size, num_heads, sequence_length, head_dim]

    # Add head dimension to K and V (Broadcast across all heads)
    K = K.unsqueeze(1) # [batch_size, 1, sequence_length, head_dim]
    V = V.unsqueeze(1) # [batch_size, 1, sequence_length, head_dim]

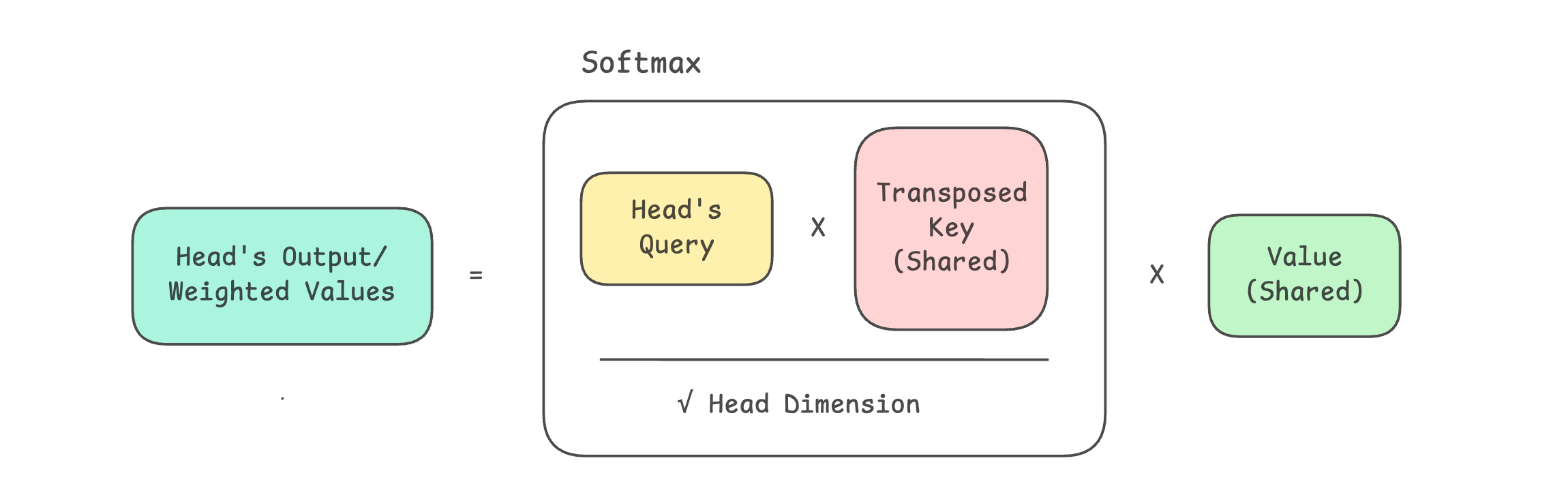
    # Calculate scaled dot-product attention
    attn_scores = Q @ K.transpose(-2, -1)
    attn_scores = attn_scores / math.sqrt(self.head_dim)

    # Create lower triangular matrix as causal masking
    causal_mask = torch.tril(torch.ones(sequence_length, sequence_length, device=x.device))

    # Add batch_size and num_heads dimensions
    causal_mask = causal_mask.view(1, 1, sequence_length, sequence_length)

    # Mask out future positions by setting their scores to -inf
    attn_scores = attn_scores.masked_fill(causal_mask == 0, float('-inf'))

    # Apply softmax to get attention weights
    attn_weights = torch.softmax(attn_scores, dim = -1)

    # Multiply attention weights by V
    weighted_values = attn_weights @ V

    # Merge head outputs
    merged_heads_output = self._merge_heads(weighted_values)

    # Obtain final output
    output = self.W_o(merged_heads_output)

    return output

This is where the magic takes place.

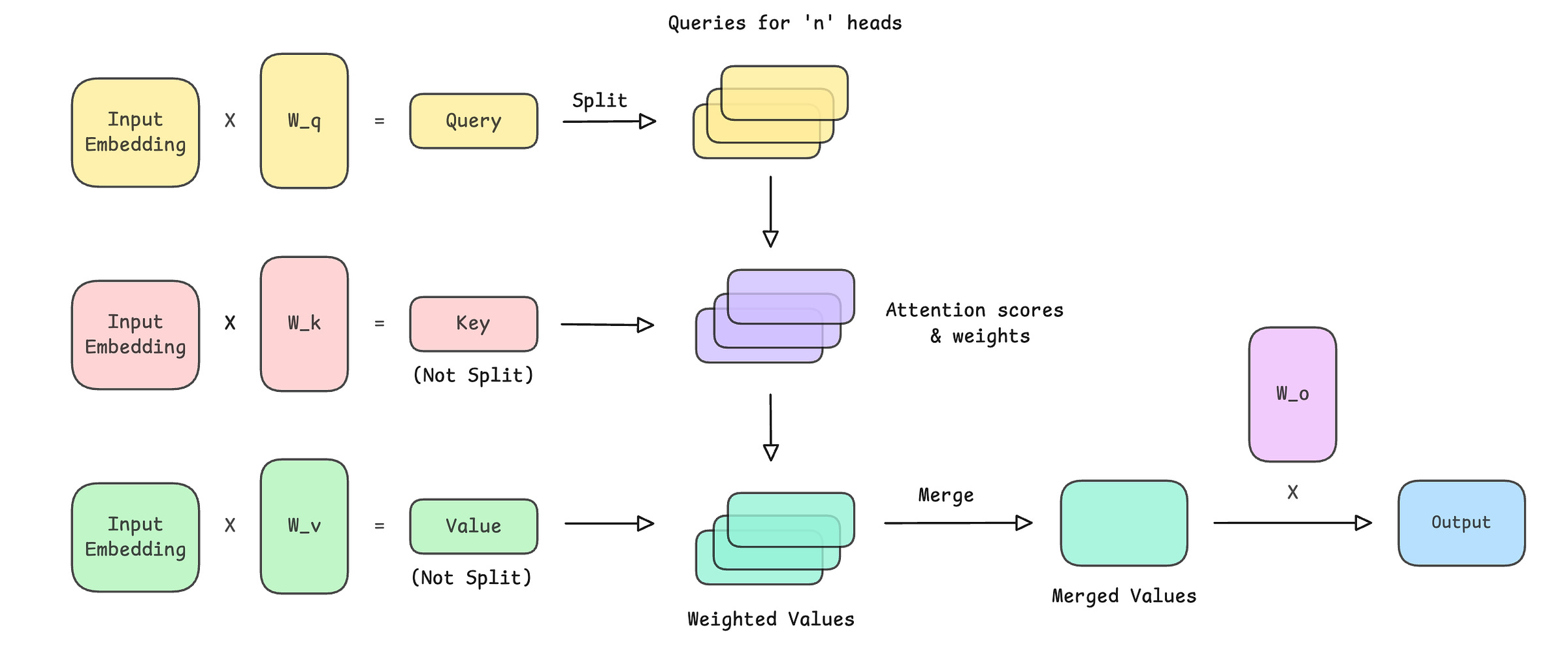
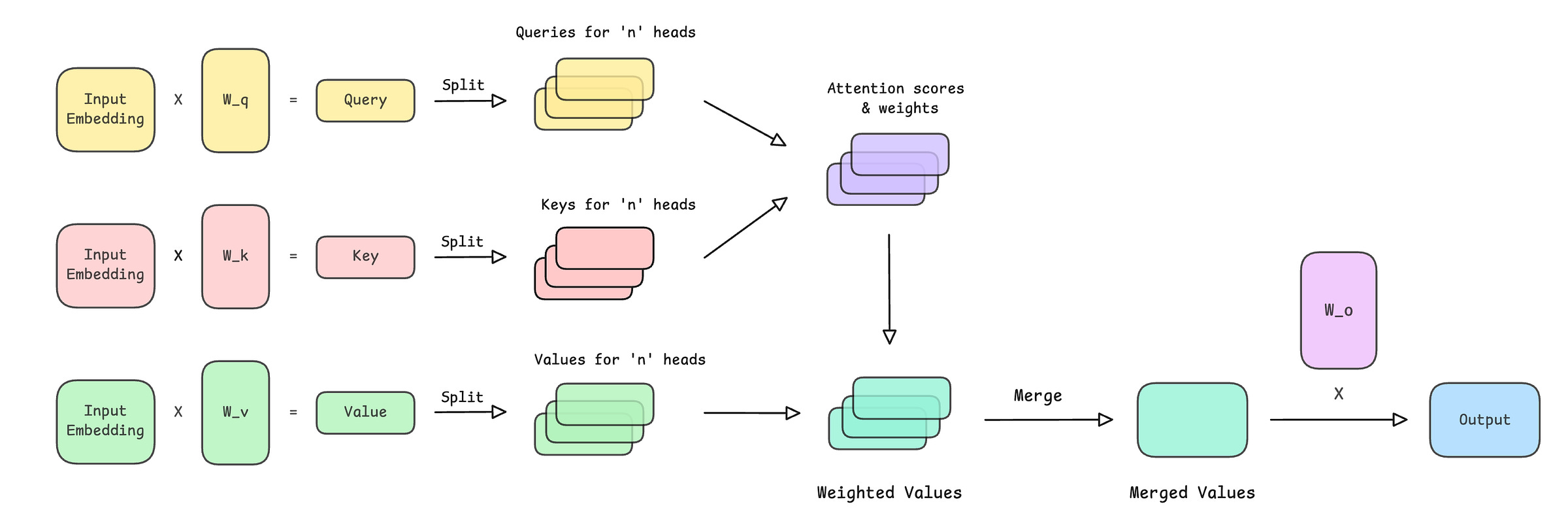
• Input embeddings are first projected into query (Q), key (K), and value (V) vectors

• The query vector is split across multiple attention heads

• The shared keys and values are broadcast across all heads

• Each head computes scaled dot-product attention scores between Q and K

• A causal mask is applied to prevent the model from attending to future tokens

• Softmax converts the masked scores into attention weights

• Attention weights are used to compute a weighted sum of values (V)

• The outputs from all heads are merged into a single representation

• A final output projection matrix produces the layer’s output

The code for the complete MultiQueryAttention class is as follows.

import torch
import torch.nn as nn
import math

class MultiQueryAttention(nn.Module):
  def __init__(self, embedding_dim, num_heads):
    super().__init__()

    # Check if embedding_dim is divisible by num_heads
    assert embedding_dim % num_heads == 0, "embedding_dim must be divisible by num_heads"

    # Embedding dimension
    self.embedding_dim = embedding_dim

    # Number of total heads
    self.num_heads = num_heads

    # Dimension of each head
    self.head_dim = embedding_dim // num_heads

    # Linear projection matrix for Query
    self.W_q = nn.Linear(embedding_dim, embedding_dim, bias = False)

    # Linear projection matrices for Key and Value
    self.W_k = nn.Linear(embedding_dim, self.head_dim, bias = False)
    self.W_v = nn.Linear(embedding_dim, self.head_dim, bias = False)

    # Linear projection matrix to produce final output
    self.W_o = nn.Linear(embedding_dim, embedding_dim, bias = False)

  # Splits Query into multiple heads
  def _split_heads(self, x):
    """
    Transforms input embeddings from
    [batch_size, sequence_length, embedding_dim]
    to
    [batch_size, num_heads, sequence_length, head_dim]
    """
    batch_size, sequence_length, embedding_dim = x.shape

    # Split embedding_dim into (num_heads, head_dim)
    x = x.reshape(batch_size, sequence_length, self.num_heads, self.head_dim)

    # Reorder and return the intended shape
    return x.transpose(1,2)

  # Merge heads back together
  def _merge_heads(self, x):
    """
    Transforms inputs from
    [batch_size, num_heads, sequence_length, head_dim]
    to
    [batch_size, sequence_length, embedding_dim]
    """
    batch_size, num_heads, sequence_length, head_dim = x.shape

    # Move sequence_length back before num_heads in the shape
    x = x.transpose(1,2)

    # Merge (num_heads, head_dim) back into embedding_dim
    embedding_dim = num_heads * head_dim
    x = x.reshape(batch_size, sequence_length, embedding_dim)

    return x

  # Forward pass
  def forward(self, x):
    batch_size, sequence_length, embedding_dim = x.shape

    # Compute Q, K, V
    Q = self.W_q(x) # [batch_size, sequence_length, embedding_dim]
    K = self.W_k(x) # [batch_size, sequence_length, head_dim]
    V = self.W_v(x) # [batch_size, sequence_length, head_dim]

    # Split Q into multiple heads
    Q = self._split_heads(Q) # [batch_size, num_heads, sequence_length, head_dim]

    # Add head dimension to K and V (Broadcast across all heads)
    K = K.unsqueeze(1) # [batch_size, 1, sequence_length, head_dim]
    V = V.unsqueeze(1) # [batch_size, 1, sequence_length, head_dim]

    # Calculate scaled dot-product attention
    attn_scores = Q @ K.transpose(-2, -1)
    attn_scores = attn_scores / math.sqrt(self.head_dim)

    # Create lower triangular matrix as causal masking
    causal_mask = torch.tril(torch.ones(sequence_length, sequence_length, device=x.device))

    # Add batch_size and num_heads dimensions
    causal_mask = causal_mask.view(1, 1, sequence_length, sequence_length)

    # Mask out future positions by setting their scores to -inf
    attn_scores = attn_scores.masked_fill(causal_mask == 0, float('-inf'))

    # Apply softmax to get attention weights
    attn_weights = torch.softmax(attn_scores, dim = -1)

    # Multiply attention weights by V
    weighted_values = attn_weights @ V

    # Merge head outputs
    merged_heads_output = self._merge_heads(weighted_values)

    # Obtain final output
    output = self.W_o(merged_heads_output)

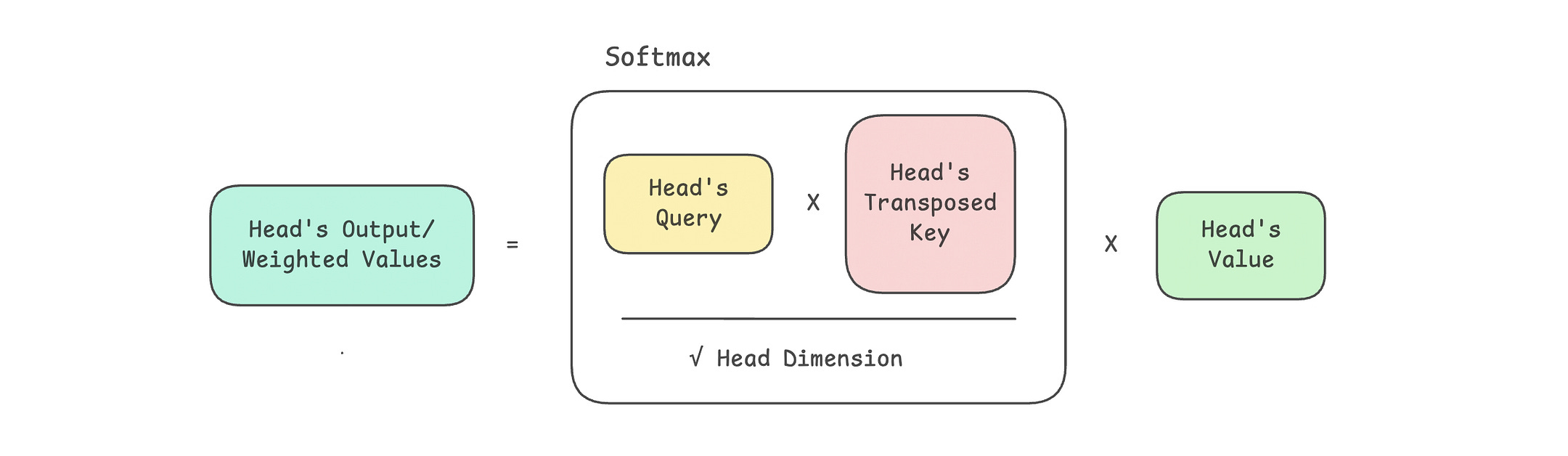
    return output

---

MQA vs. MHA Visualised

This is how the operations in MQA look.

MQA operations

MQA weighted Values calculation (Causal mask not shown)

Compare them with the operations in MHA as shown below.

MHA calculations

MHA weighted Values calculations (Causal mask not shown)

---

Testing Out MQA

Let’s use MQA to process some randomly initialized input embeddings as follows.

# Hyperparameters
batch_size = 1
sequence_length = 4
embedding_dim = 6
num_heads = 3

# Create input embeddings
input_embeddings = torch.rand(batch_size, sequence_length, embedding_dim)

# Initialize MQA
mqa = MultiQueryAttention(embedding_dim, num_heads)

# Forward pass
output = mqa(input_embeddings)

Note how MQA preserves the shape of the input ([batch_size, sequence_length, embedding_dim]) just like MHA. This lets us stack multiple MQA layers together in a Transformer block.

print("Input shape:", input_embeddings.shape)
print("Output shape:", output.shape)

"""
Output:
Input shape: torch.Size([1, 4, 6])
Output shape: torch.Size([1, 4, 6])
"""

---

If you loved reading this article and found it valuable, restack to share it with others. ❤️

---

If you want to get even more value from this publication, become a paid subscriber.

Get access to all valuable lessons, such as:

Build and Train an LLM from Scratch

20 PyTorch Concepts, Explained Simply

Build a Mixture-of-Experts (MoE) LLM from Scratch (Part-1)

Google Trained Gemini 3 Entirely Using JAX on Its TPUs: Here Is Why It Matters

---

You can also check out my books on Gumroad and connect with me on LinkedIn to stay in touch.