Build a Mixture-of-Experts (MoE) LLM from Scratch (Part-2)
Learn to build the Mixture-of-Experts (MoE) Transformer, the core architecture that powers LLMs like gpt-oss, Grok, and Mixtral, from scratch in PyTorch.
The Mixture-of-Experts (MoE) architecture is used by many modern-day LLMs like Grok-1, DeepSeekMoE, gpt-oss, and Mixtral (and many other proprietary LLMs whose architectural details aren’t publicly available).
This is because it enables sparse computation of tokens that significantly reduces the computational requirements of an LLM.
In the previous lesson on ‘Into AI’, we learned how to implement the Mixture-of-Experts (MoE) layer from scratch.
It is implemented using the class MixtureOfExpertsLayer with two functionalities:
The core MoE computation via the
forwardmethodRegularization using a load-balancing loss via the
load_balance_lossmethod
# Expert: Single expert feed-forward network
class Expert(nn.Module):
def __init__(self, embedding_dim, ff_dim, dropout = 0.1):
super().__init__()
self.fc1 = nn.Linear(embedding_dim, ff_dim)
self.activation = nn.GELU()
self.dropout = nn.Dropout(dropout)
self.fc2 = nn.Linear(ff_dim, embedding_dim)
def forward(self, x):
x = self.fc1(x) # Expand dimensions to ff_dim
x = self.activation(x) # GELU activation
x = self.dropout(x) # Dropout regularization
x = self.fc2(x) # Project back to embedding_dim
return x # Router: Network that decides which expert should process a token
class Router(nn.Module):
def __init__(self, embedding_dim, num_experts, top_k = 3):
super().__init__()
self.num_experts = num_experts
self.top_k = top_k
# Linear layer to compute router logits
self.gate = nn.Linear(embedding_dim, num_experts, bias = False)
def forward(self, x):
# Compute logits for each expert
router_logits = self.gate(x)
# Select top-k experts with the highest logits
# top_k_logits: Logit values for top-k selected experts
# top_k_indices: Indices of top-k selected experts
top_k_logits, top_k_indices = torch.topk(router_logits, self.top_k, dim=-1)
# Normalize the top-k scores into weights that sum to 1 using softmax
top_k_weights = torch.softmax(top_k_logits, dim = -1)
# For load-balancing later, convert logits to probabilities using softmax over all experts
router_probs = torch.softmax(router_logits, dim = -1)
return router_probs, top_k_indices, top_k_weights# Mixture-of-Experts layer
class MixtureOfExpertsLayer(nn.Module):
def __init__(self, embedding_dim, ff_dim, num_experts, top_k, dropout=0.1):
super().__init__()
# Each token must pick at least one expert and at most num_experts
assert 1 <= top_k <= num_experts, "top_k must be between 1 and num_experts"
self.embedding_dim = embedding_dim
self.num_experts = num_experts
self.top_k = top_k
# Router
self.router = Router(embedding_dim, num_experts, top_k)
# Experts
self.experts = nn.ModuleList([
Expert(embedding_dim, ff_dim, dropout)
for _ in range(num_experts)
])
def load_balance_loss(self, router_probs, top_k_indices):
# Dimensions
total_tokens, total_experts = router_probs.shape
# Importance: average router probability for each expert across all tokens
importance = router_probs.mean(dim=0)
# Load: fraction of all expert slots assigned to each expert
all_selected_experts = top_k_indices.reshape(-1)
load = (
torch.bincount(all_selected_experts, minlength=total_experts)
.float() / (total_tokens * self.top_k)
)
# Loss encourages uniform distribution across experts
loss = total_experts * (importance * load).sum()
return loss
def forward(self, x):
batch_size, sequence_length, embedding_dim = x.shape
# Flatten batch and sequence dimensions to route per token
num_tokens = batch_size * sequence_length
x_flat = x.reshape(num_tokens, embedding_dim)
# Router outputs
router_probs, top_k_indices, top_k_weights = self.router(x_flat)
# Initialize output tensor to accumulate expert outputs
output = torch.zeros_like(x_flat)
# Process each expert separately (sparse computation)
for expert_id in range(self.num_experts):
# Mask to find which tokens selected this expert
mask = (top_k_indices == expert_id)
# Skip this expert if no tokens are routed to it
if not mask.any():
continue
# Extract positions where this expert was selected
# token_ids: which tokens need this expert
# k_positions: which top-k slot this expert occupies (e.g. 0, 1, or 2 for top-3)
token_ids, k_positions = mask.nonzero(as_tuple=True)
# Get embeddings for tokens that selected this expert
expert_input = x_flat[token_ids]
# Forward pass through the expert
expert_output = self.experts[expert_id](expert_input)
# Get routing weights for this expert's contribution
weights = top_k_weights[token_ids, k_positions].unsqueeze(-1)
# Add this expert's weighted output to the final output
output[token_ids] += expert_output * weights
# Compute load-balancing auxiliary loss
aux_loss = self.load_balance_loss(router_probs, top_k_indices)
# Reshape from (num_tokens, embedding_dim) back to original dimensions
output = output.reshape(batch_size, sequence_length, embedding_dim)
return output, aux_lossIn this lesson, we will learn to integrate this layer into the Decoder-only Transformer architecture to create a Mixture-of-Experts Transformer.
Let’s begin!
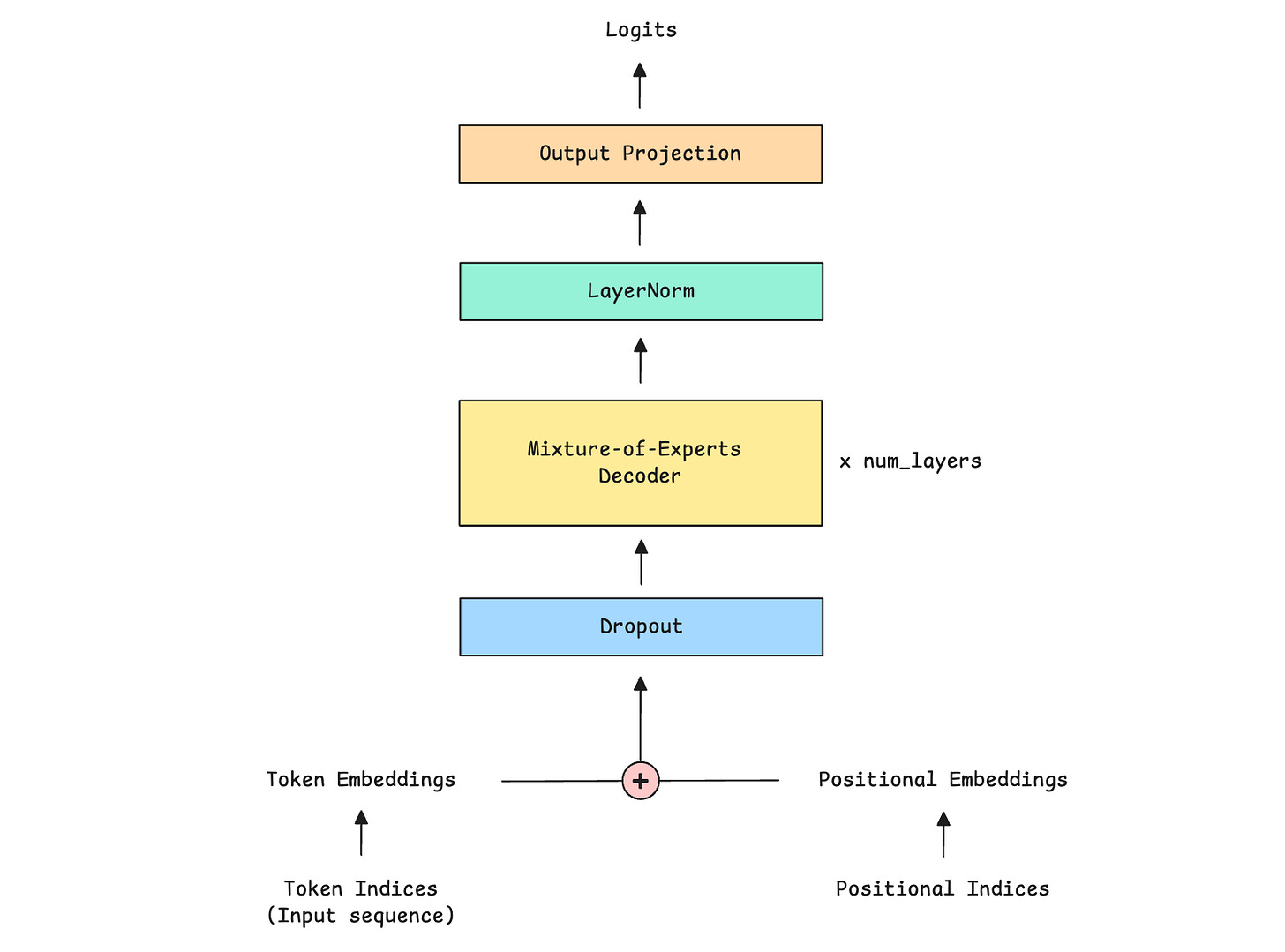
Building the Mixture-of-Experts Decoder
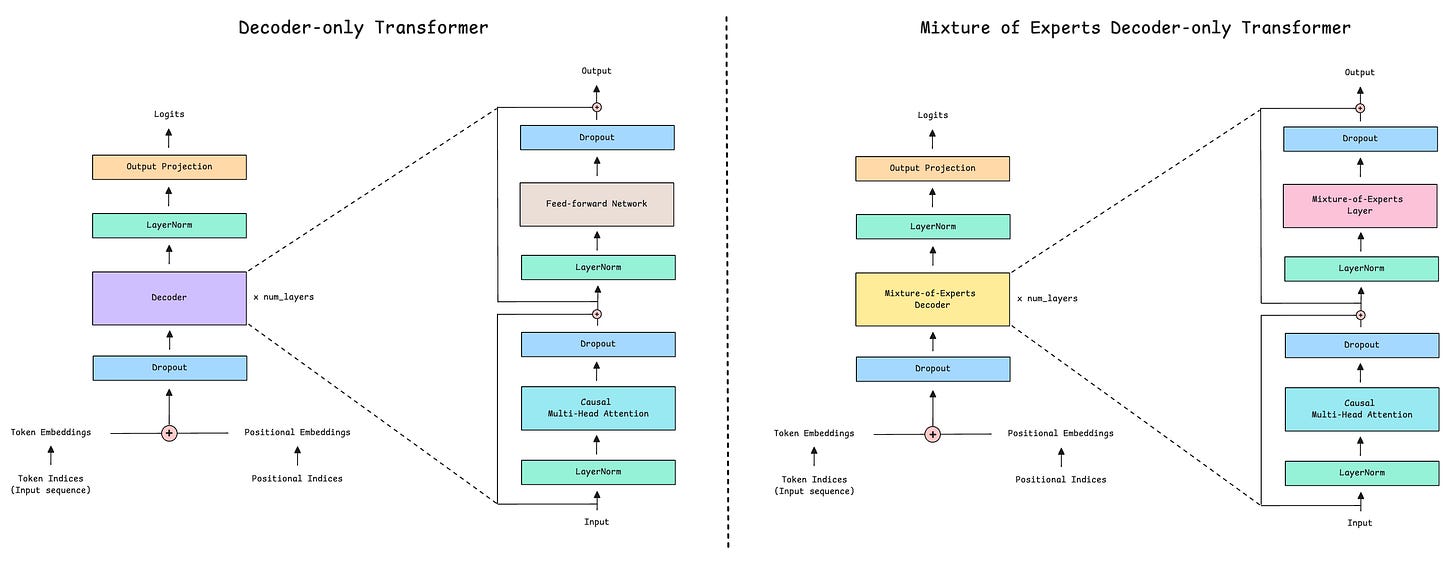
The conventional Decoder-only Transformer architecture consists of the following components:
Causal (or Masked) Multi-Head Self-Attention
Feed-Forward Network (FFN)
Layer Normalization
Residual or Skip connections
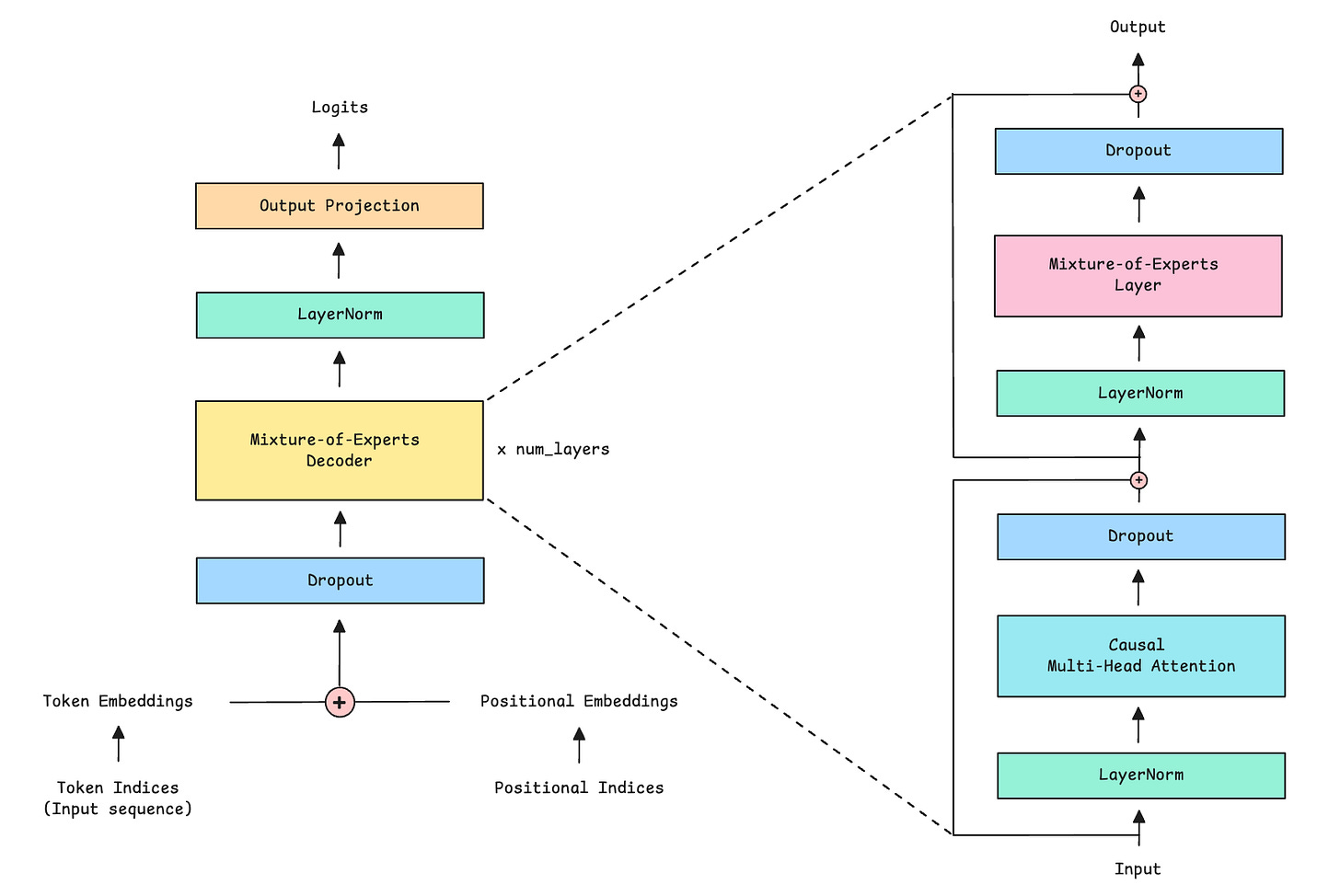
In the Mixture-of-Experts (MoE) architecture, the feed-forward network (FFN) is simply replaced by the Mixture-of-Experts layer.
Let’s first implement the Mixture-of-Experts (MoE) Decoder in PyTorch, as shown below.
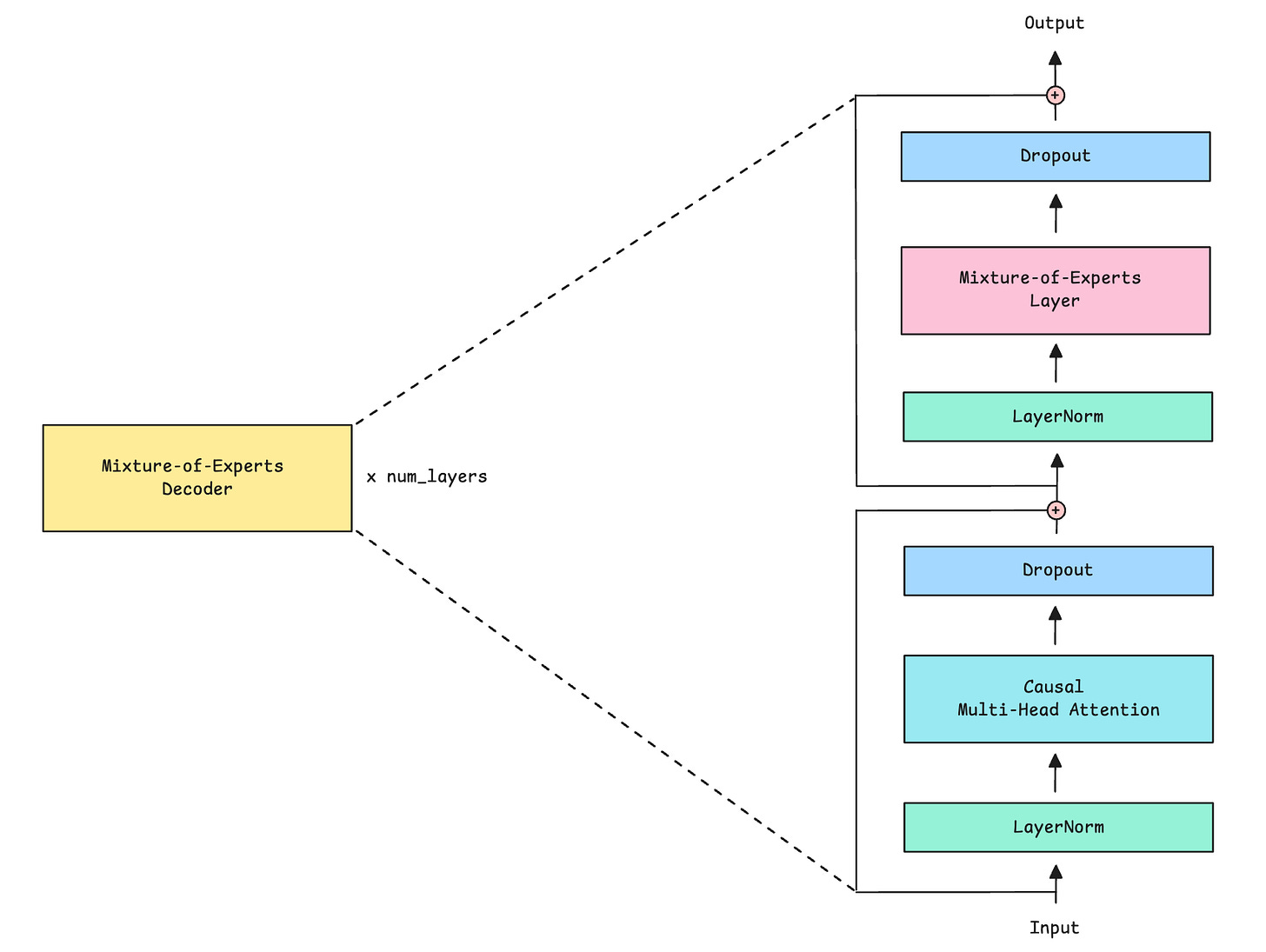
The class MixtureOfExpertsDecoder implements the MoE Decoder, where:
We first apply Causal multi-head self-attention to the inputs
Next, we pass the outputs through the MoE layer
Both components use Pre-LayerNorm, which means that normalization happens before rather than after each sub-layer
Both also use Residual connections (adding the input back to the output) and Dropout to improve training stability.
Along with its output, the MoE Decoder also returns an auxiliary load-balancing loss to encourage balanced expert use during training. We discussed this loss in depth in the last lesson.
# Causal Multi-head Self-attention
class CausalMultiHeadSelfAttention(nn.Module):
def __init__(self, embedding_dim, num_heads):
super().__init__()
assert embedding_dim % num_heads == 0, "embedding_dim must be divisible by num_heads"
self.embedding_dim = embedding_dim
self.num_heads = num_heads
self.head_dim = embedding_dim // num_heads
self.W_q = nn.Linear(embedding_dim, embedding_dim, bias=False)
self.W_k = nn.Linear(embedding_dim, embedding_dim, bias=False)
self.W_v = nn.Linear(embedding_dim, embedding_dim, bias=False)
self.W_o = nn.Linear(embedding_dim, embedding_dim, bias=False)
def _split_heads(self, x):
batch_size, sequence_length, embedding_dim = x.shape
x = x.reshape(batch_size, sequence_length, self.num_heads, self.head_dim)
return x.transpose(1, 2)
def _merge_heads(self, x):
batch_size, num_heads, sequence_length, head_dim = x.shape
x = x.transpose(1, 2)
embedding_dim = num_heads * head_dim
x = x.reshape(batch_size, sequence_length, embedding_dim)
return x
def forward(self, x):
batch_size, sequence_length, embedding_dim = x.shape
Q = self.W_q(x)
K = self.W_k(x)
V = self.W_v(x)
Q = self._split_heads(Q)
K = self._split_heads(K)
V = self._split_heads(V)
attn_scores = Q @ K.transpose(-2, -1)
attn_scores = attn_scores / math.sqrt(self.head_dim)
causal_mask = torch.tril(torch.ones(sequence_length, sequence_length, device=x.device))
causal_mask = causal_mask.view(1, 1, sequence_length, sequence_length)
attn_scores = attn_scores.masked_fill(causal_mask == 0, float("-inf"))
attn_weights = torch.softmax(attn_scores, dim=-1)
weighted_values = attn_weights @ V
merged_heads_output = self._merge_heads(weighted_values)
output = self.W_o(merged_heads_output)
return output# Mixture-of-Experts Decoder
"""
A Decoder that combines:
1. Causal Multi-Head Self-Attention
2. MoE layer
"""
class MixtureOfExpertsDecoder(nn.Module):
def __init__(self, embedding_dim, ff_dim, num_heads, num_experts, top_k, dropout = 0.1):
super().__init__()
# Causal multi-head self-attention
self.attention = CausalMultiHeadSelfAttention(embedding_dim, num_heads)
# Mixture-of-experts layer
self.moe_layer = MixtureOfExpertsLayer(
embedding_dim = embedding_dim,
ff_dim = ff_dim,
num_experts = num_experts,
top_k = top_k,
dropout = dropout)
# Pre-LayerNorm
self.ln1 = nn.LayerNorm(embedding_dim) # LayerNorm before attention
self.ln2 = nn.LayerNorm(embedding_dim) # LayerNorm before MoE layer
# Dropout
self.dropout = nn.Dropout(dropout)
def forward(self, x):
# Self-Attention with residual connection
attn_output = self.attention(self.ln1(x))
x = x + self.dropout(attn_output)
# MoE layer with residual connection
moe_output, aux_loss = self.moe_layer(self.ln2(x))
x = x + self.dropout(moe_output)
return x, aux_lossBuilding the Mixture-of-Experts Transformer
It’s finally time to build the complete Mixture-of-Experts Transformer, as shown below.
It is implemented as the MixtureOfExpertsTransformer class.
The class first sets up all necessary components, which include:
Token embedding layer to convert token indices to embedding
Positional embedding layer to encode sequence positions to positional embedding
Dropout layer for regularization
Multiple MoE decoders, where each decoder contains both the Causal Multi-head self-attention mechanism and the Mixture-of-experts layer.
Layer normalization component
Output projection layer that transforms the final hidden states back to the vocabulary size
The forward pass involves taking the following steps:
Validate that the given input sequence length doesn’t exceed the maximum sequence length that the model can process (
max_seq_length)Generates positional indices
Converts token indices and positions to embeddings
Combine token and positional embeddings and apply Dropout
Pass the inputs through each MoE decoder sequentially and collect auxiliary losses
Apply final layer normalization
Project the result to vocabulary size to get logits
Average the auxiliary losses and scale by the coefficient (
moe_aux_loss_coef)Return logits and the load-balancing auxiliary loss
# MoE Decoder-only Transformer
class MixtureOfExpertsTransformer(nn.Module):
def __init__(
self,
vocab_size, # Total number of tokens in the vocabulary
embedding_dim, # Token embedding dimension
num_heads, # Number of attention heads in each decoder
ff_dim, # Hidden dimension of experts
num_layers, # Number of stacked MoE decoders
max_seq_length, # Max input sequence length the model can handle
num_experts = 8, # Total number of experts per MoE layer
top_k = 3, # Number of experts to activate per token
dropout = 0.1, # Dropout
moe_aux_loss_coef = 0.01, # Coefficient for auxiliary load balancing loss
):
super().__init__()
self.max_seq_length = max_seq_length
self.moe_aux_loss_coef = moe_aux_loss_coef
# Token embedding layer
self.token_embedding = nn.Embedding(vocab_size, embedding_dim)
# Learned positional embedding layer
self.positional_embedding = nn.Embedding(max_seq_length, embedding_dim)
# Dropout
self.dropout = nn.Dropout(dropout)
# Stack of MoE decoders (total: 'num_layers')
self.decoders = nn.ModuleList([
MixtureOfExpertsDecoder(
embedding_dim,
ff_dim,
num_heads,
num_experts,
top_k,
dropout
)
for _ in range(num_layers)
])
# Final Layer Normalization layer
self.final_ln = nn.LayerNorm(embedding_dim)
# Linear layer to project hidden states to vocabulary size to get logits
self.output_proj = nn.Linear(embedding_dim, vocab_size)
def forward(self, x):
# x is token indices/ input sequence of shape (batch_size, sequence_length)
batch_size, sequence_length = x.shape
# Check that sequence length does not exceed maximum
if sequence_length > self.max_seq_length:
raise ValueError(f"Input sequence length {sequence_length} exceeds maximum sequence length {self.max_seq_length}.")
# Create positional indices: [0, 1, 2, ..., sequence_length-1]
positions = torch.arange(sequence_length, device=x.device)
# Create token embedding from token indices
token_embedding = self.token_embedding(x)
# Create positional embedding from positional indices
positional_embedding = self.positional_embedding(positions)
# Combine embeddings and add Dropout
x = self.dropout(token_embedding + positional_embedding)
# Array to store auxiliary losses from each MoE decoder
aux_losses = []
# Forward pass through MoE decoders sequentially
for decoder in self.decoders:
x, aux_loss = decoder(x)
aux_losses.append(aux_loss)
# Apply LayerNorm to the output
x = self.final_ln(x)
# Project to vocabulary size to get logits for next-token prediction
logits = self.output_proj(x)
# Mean auxiliary losses across all MoE decoders and scale by coefficient
aux_loss = torch.stack(aux_losses).mean() * self.moe_aux_loss_coef
return logits, aux_lossThis completes our Decoder-only Mixture-of-Experts Transformer.
Inference from the Mixture-of-Experts Transformer
It’s time to define some hyperparameters, instantiate our Mixture-of-Experts Transformer model, and test its outputs.
# Hyperparameters
vocab_size = 50257
embedding_dim = 768
ff_dim = 3072 # 4 × embedding_dim
num_heads = 12
num_layers = 12
max_seq_length = 1024
num_experts = 8
top_k = 3
batch_size = 2
sequence_length = 128
# Create model
model = MixtureOfExpertsTransformer(
vocab_size = vocab_size,
embedding_dim = embedding_dim,
num_heads = num_heads,
ff_dim = ff_dim,
num_layers = num_layers,
max_seq_length = max_seq_length,
num_experts = num_experts,
top_k = top_k,
dropout = 0.1,
moe_aux_loss_coef = 0.01
)The total number of parameters in our model is 559.81 million, which is calculated as follows.
# Check model parameters
trainable_params = sum(p.numel() for p in model.parameters() if p.requires_grad)
total_params = sum(p.numel() for p in model.parameters())
print(f"Trainable parameters: {trainable_params:,} ({trainable_params/1e6:.2f}M)")
print(f"Total parameters: {total_params:,} ({total_params/1e6:.2f}M)\n")
"""
Output:
Trainable parameters: 559,808,593 (559.81M)
Total parameters: 559,808,593 (559.81M)
"""Our model looks as follows.
print(model)
"""
Output:
MixtureOfExpertsTransformer(
(token_embedding): Embedding(50257, 768)
(positional_embedding): Embedding(1024, 768)
(dropout): Dropout(p=0.1, inplace=False)
(decoders): ModuleList(
(0-11): 12 x MixtureOfExpertsDecoder(
(attention): CausalMultiHeadSelfAttention(
(W_q): Linear(in_features=768, out_features=768, bias=False)
(W_k): Linear(in_features=768, out_features=768, bias=False)
(W_v): Linear(in_features=768, out_features=768, bias=False)
(W_o): Linear(in_features=768, out_features=768, bias=False)
)
(moe_layer): MixtureOfExpertsLayer(
(router): Router(
(gate): Linear(in_features=768, out_features=8, bias=False)
)
(experts): ModuleList(
(0-7): 8 x Expert(
(fc1): Linear(in_features=768, out_features=3072, bias=True)
(activation): GELU(approximate='none')
(dropout): Dropout(p=0.1, inplace=False)
(fc2): Linear(in_features=3072, out_features=768, bias=True)
)
)
)
(ln1): LayerNorm((768,), eps=1e-05, elementwise_affine=True)
(ln2): LayerNorm((768,), eps=1e-05, elementwise_affine=True)
(dropout): Dropout(p=0.1, inplace=False)
)
)
(final_ln): LayerNorm((768,), eps=1e-05, elementwise_affine=True)
(output_proj): Linear(in_features=768, out_features=50257, bias=True)
)
"""Next, we create an input sequence to pass through the model.
In real training or inference, the input sequences are generated by tokenizing actual data, but for this tutorial, we will initialize an input sequence with random values.
# Sample input sequence with random token indices: 2D tensor of shape (batch_size, sequence_length) of random integer token IDs
input_tokens = torch.randint(0, vocab_size, (batch_size, sequence_length))Let’s run a forward pass of the input sequence through our model and obtain an output.
# Forward pass
with torch.no_grad():
logits, aux_loss = model(input_tokens)
print(f"Output logits shape: {logits.shape}")
print(f"Auxiliary loss: {aux_loss.item():.6f}")The model outputs logits for all positions in the input sequence, along with the auxiliary loss.
The shapes of the model's input and output logits, and the auxiliary loss value, are as follows.
print(f"Input shape: {input_tokens.shape}\n")
print(f"Output logits shape: {logits.shape}\n")
print(f"Auxiliary loss: {aux_loss.item():.6f}")
"""
Output:
Input shape: torch.Size([2, 128]) # (batch_size, sequence_length)
Output logits shape: torch.Size([2, 128, 50257]) # (batch_size, sequence_length, vocab_size)
Auxiliary loss: 0.010084
"""To generate the next token from the input sequence/ inference, we first disable gradient tracking torch.no_grad()and then obtain the logits for the last position.
We convert these logits into a probability distribution using softmax, where higher logits correspond to higher probabilities and all probabilities sum to 1.
We use the argmax method to select the token with the highest probability (Greedy decoding). This gives us the predicted next token index for each sequence in the batch.
Finally, we extract and display the top-5 most probable tokens, along with their probabilities, for both batches to see which alternatives the model considered.
with torch.no_grad(): # Disable tracking gradients (no backpropagation)
last_logits = logits[:, -1, :] # Logits for last position only
last_probs = torch.softmax(last_logits, dim=-1) # Convert to probabilities
next_token = torch.argmax(last_probs, dim=-1) # Pick highest probability token (Greedy decoding)
print(f"Predicted next token indices: {next_token}\n")
print(f"Next token shape: {next_token.shape}\n")
print(f"Top-5 probabilities for first batch:")
top5_probs, top5_indices = torch.topk(last_probs[0], 5)
for i, (prob, idx) in enumerate(zip(top5_probs, top5_indices)):
print(f" {i+1}. Token {idx.item()}: {prob.item():.4%}")
print(f"\nTop-5 probabilities for second batch:")
top5_probs, top5_indices = torch.topk(last_probs[1], 5)
for i, (prob, idx) in enumerate(zip(top5_probs, top5_indices)):
print(f" {i+1}. Token {idx.item()}: {prob.item():.4%}")
"""
Output:
Predicted next token indices: tensor([38018, 13421])
Next token shape: torch.Size([2])
Top-5 probabilities for first batch:
1. Token 38018: 0.0177%
2. Token 16010: 0.0167%
3. Token 44662: 0.0159%
4. Token 12541: 0.0148%
5. Token 10099: 0.0145%
Top-5 probabilities for second batch:
1. Token 13421: 0.0238%
2. Token 31662: 0.0181%
3. Token 8611: 0.0179%
4. Token 13436: 0.0171%
5. Token 37508: 0.0165%
"""Since we have not trained our model, and its weights are randomly initialized, these outputs are random and meaningless. We will discuss model training in an upcoming lesson.
That’s everything for this article. Thanks for reading it!
If you are struggling to understand this article well, start with the previous lessons in this series:
If you found it valuable, share this article with others ❤️
If you want to get even more value from this publication and support me in creating these in-depth tutorials, consider becoming a paid subscriber.
You can also check out my books on Gumroad and connect with me on LinkedIn to stay in touch.






Regarding the topic of the article, this is exactly what I needed after Part 1! That first lesson on the MoE layer was super clear, and now seeing how the router and expert classes connect for the full LLM build makes so much sense. Prety insightful stuff, Dr. Bamania!